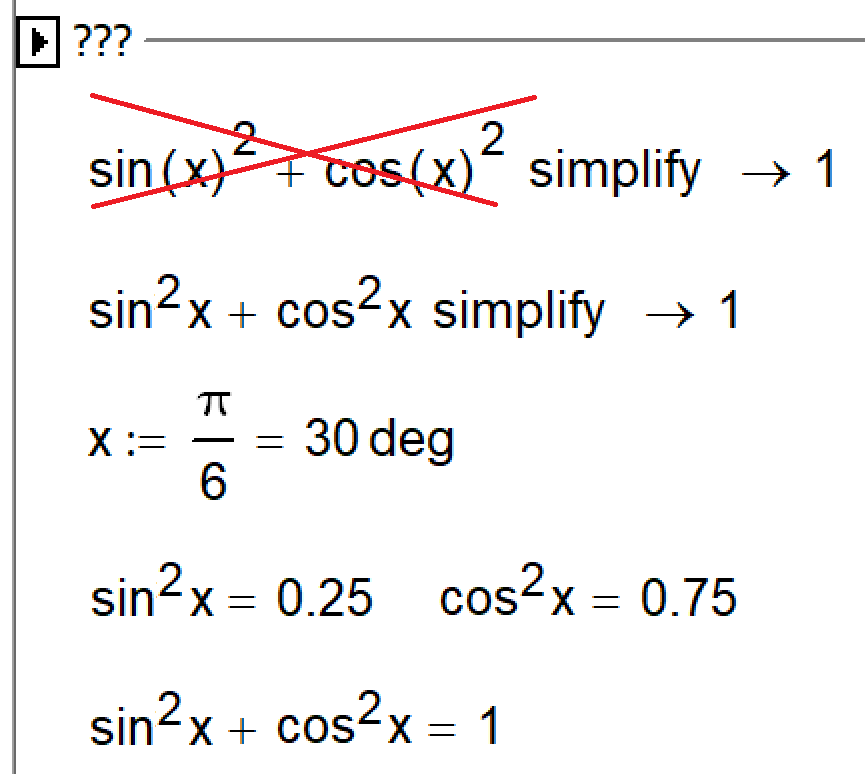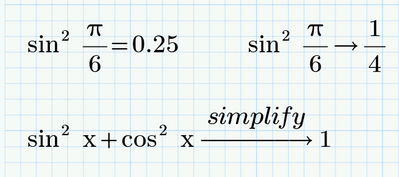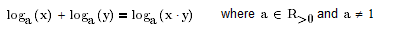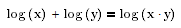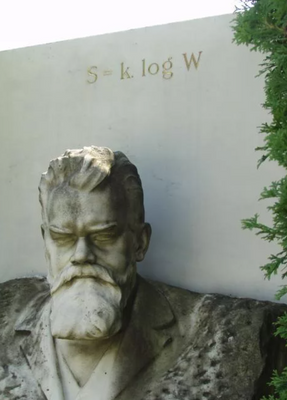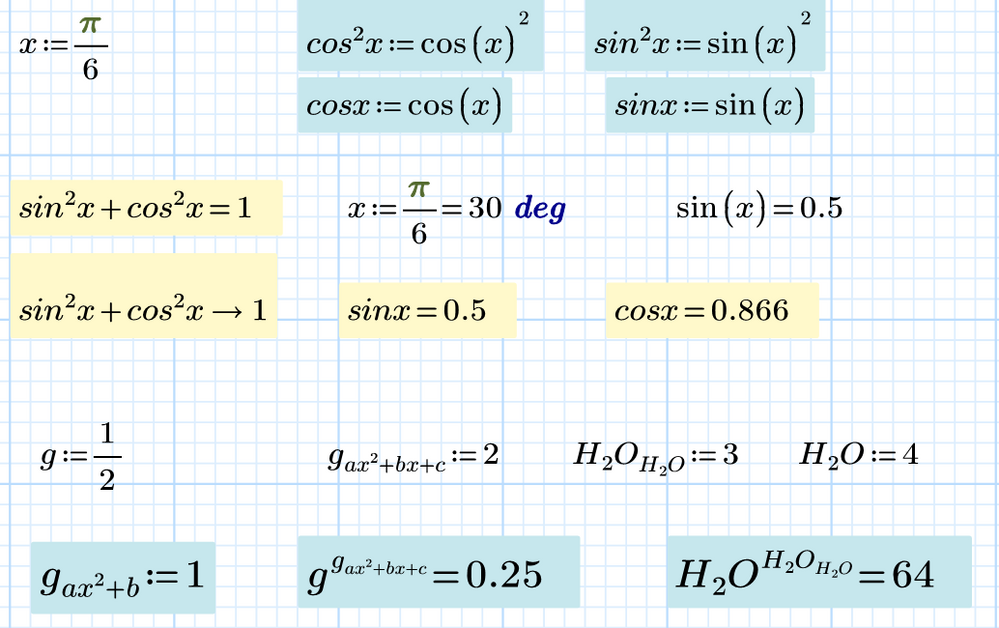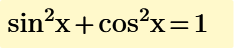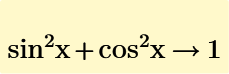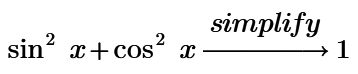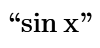- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Formulas in Mathcad and textbooks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Formulas in Mathcad and textbooks
The writing of some formulas in Mathcad differs from the writing of these formulas in textbooks in mathematics.
My students have learned to partially correct this.
One example is in the picture.
Three questions.
1. Guess how my students do it! What is written in the hidden area.
2. Show other examples of such a mismatch of operators in Mathcad and textbooks.
3. What needs to be changed - Mathcad or textbooks?
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It goes without saying that its not the textbooks which should be changed, of course.
And Mathcads way of showing the square of the sine and cosine is perfectly compliant with the ISO80000-2. Omitting the parentheses and putting the exponent right after the functions name is allowed for named functions which also have a named inverse (and also preferred by me in that case) but its not mandatory.
The standards would also allow something like
BTW, try your workaround in Prime where we don't have the comfort of the Prefix Operator 😉
To conform with the standards we would of course have to change the standard Prime display to use an upright font without serifs.
And as you ask for other examples: The usage of "log" for the decadic logarithm "lg" is wrong! According to the standards "log" is neither the decadic nor the natural logarithm but should only be used to represent a generic logarithm, e.g. to demonstrate a log rule.
So instead of writing
you may simply write
but thats it. There is nothing like log(100)=2.
BTW, quite some lecture notes and even some textbooks use "log" for the natural logarithm "ln" which of course is incorrect, too.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One of my students solved numerically the differential equations in Mathcad, and then checked it by solving the problem analytically on Wolframalppa website. The answer didn't match. The student struggled with the task until he realized that in Mathcad log is decimal, and in Mathematica it is natural.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
One of my students solved numerically the differential equations in Mathcad, and then checked it by solving the problem analytically on Wolframalppa website. The answer didn't match. The student struggled with the task until he realized that in Mathcad log is decimal, and in Mathematica it is natural.
And both programs are doing wrong and do not respect the standards. This ignorance is not understandable.
Mathematica is famous for using non-standard own notations - just think of Sin[x] instead of sin(x) or the wrong Sin^-1[x] instead of arcsin(x). asin(x)as used by Mathcad is often seen in publications, but its not compliant to the current standards. Using sin^-1(x) as is often used by school pupils is definitely wrong. If this would be a valid notation for the inverse of the sine function, we would not be allowed to write sin²(x) or sin² x for the square of the sine function.
The inverse of a generic function named f(x) is to be named f^-1(x) but you are not allowed to write f²(x) for the square but must write f(x)² or (to be on the safe side as many people think that the argument is squared that way) (f(x))².
But the rule is that if the function and its inverse have special defined names (like sin and arcsin) these names must be used but for this we may use the convenient notation for the powers.
The rule is not really clever if you remember that f^-1(x) ist the inverse of the function f(x), but sin^-1(x) is the reciprocal of sin(x). Its even worse in German, where the very easily confused expressions "Umkehrung" (for inverse) and "Kehrwert" (for reciprocal) are common.
Wish the standards would have chosen a different notation for the inverse of a generic function f(x).
I remember when I was first confronted with inverse functions at school, the notation we used was f*(x) and not f^-1(x) but we soon had to switch over to the other notation.
OK, when first heard about the set of natural numbers, zero wasn't in that set. It was only somewhere in the 1970's when the standards were changed and since then zero is a natural number, too. Guess I am showing my age ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>Mathematica is famous for using non-standard own notations.
Boltzmann used Mathematica for calculations, not Mathcad.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Boltzmann died 1906, ISO was founded 1947 in London. Boltzmann didn't even have the opportunity to adhere to international standards because there simply weren't any. 😉
By the way, the tomb and the bust were cleaned in the meantime 🙂
https://upload.wikimedia.org/wikipedia/commons/5/58/Ludwig_Boltzmann_Grave_Zentralfriedhof_Vienna_2022.jpg
Nowadays we would write the equation (which actually stems from Max Planck based on ideas from Boltzmann) like
And here is Boltzmann, resurrected, studying the current standards online and being fascinated by the possibilities offered by today's technology
And if you are a fan, you sure need this: SKLOGW
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

From my book "Leo Tolstoy and Math" " (mpei.ac.ru)
Leo Tolstoy and Ludwig Boltzmann are similar externally and internally. Both in their young and not very young years were revelers, both married young people, both gave birth to a bunch of kids, both wore bushy beards in their mature years, and both, alas, ended their lives tragically. Boltzmann committed suicide. Tolstoy, as many believe, also actually carried out an act of suicide, but not instantaneous, but stretched out for a week. Both have unusual graves. Tolstoy has a modest mound in the forest. Boltzmann has his famous formula S = k lnW engraved on his gravestone, relating the entropy S of a thermodynamic state to the number of corresponding microstates W (log (decimal logarithm) is engraved on the monument instead of ln (natural logarithm), since the second spelling appeared only 13 years after Boltzmann's death). In addition, many mathematicians quite reasonably believe that there is only one natural logarithm, and the decimal logarithm is some kind of temporary construction designed to facilitate manual calculations (think of the slide rule, which we already mentioned). The parameter k in the Boltzmann formula is the Boltzmann constant, one of several fundamental constants (Planck's constant, Avogadro's number, etc.) on which modern physics is based. Boltzmann's forerunner in the discovery of molecular kinetic theory was Maxwell (1831–1879). You will laugh, but he also wore a bushy beard with a shovel. Maybe it's all about the beard?!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
log (decimal logarithm) is engraved
No! "log" is neither the decadic nor the natural logarithm (according to the standards) "log" is written on most pocket calculators instead of "lg", but TI, Casio & co. are not standardization institutes! The also write sin^-1 etc on the keys of their devices which isn't correct either but leads pupils to use this term instead of the correct one.
Maybe it's all about the beard?!
Too late! I should have known earlier 😞
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
On the other side of this grave monument, the text will be written in an attachment.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
sinx - without any space???
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I can make bellow, but I can't find how to make sin x.