Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Fraction and Unit Fractions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fraction and Unit Fractions.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Happy to be able to post again (although severely hampered by this "moderation" delay), here are some more solutions to your third task.
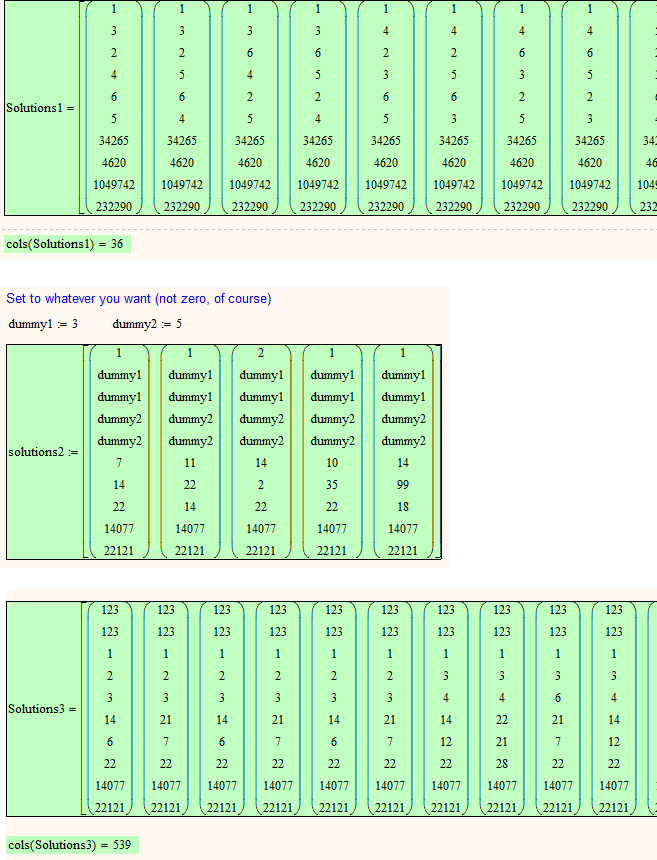
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
May be this is the "help":
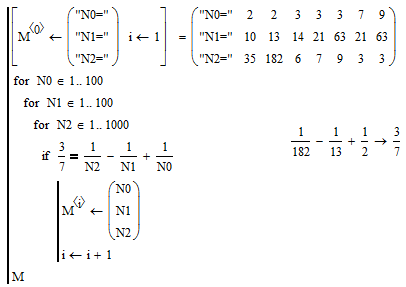
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery, try your method to find solutions for Loi's third problem 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guess you would have to write some routines to try "all" possibilities.
Using a generic brute force program I wrote some time ago I found some solutions for your first two problems.
Solutions with the smallest possible integers are
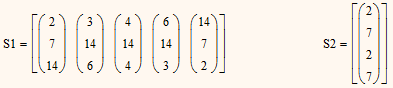
but if you allow bigger integers you get a lot more solutions. Below are the solutions for task 1 with integers from 1 to 200 and task to for the range 1 to 100.

As for the third problem, the denominator 2011 is a prime and so without amore intelligent algorithm we would have to try all numbers from 1 to 2011 at least. Probably there would be no solution found and we should try up to integer multiples of 2011. Trying all numbers from 1 to 2011 would mean we have to try 4^2011=5*10^29 times. Based on the timing with a smaller range this would take on my machine about 10^18 years!!
So problem 3 would require more thinking and less brute force.
Addendum: Here is one (of sure many) solution for your third problem, found by a different method, of course

Thats my second post after PTC introduced its "moderation" of all posts. The first was sent 6 hours ago and still is not open for public. Could image that if that kind of moderation stays, that I will go.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Happy to be able to post again (although severely hampered by this "moderation" delay), here are some more solutions to your third task.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello, again.
Thanks in advance for the time and help.
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the meantime you should know that Mathcads solve block can hardly be convinced to give integer solutions and you would have to write some program routines to get solutions - which is sometimes possible, sometimes not.
Why don't you attach a sheet to show what programs you have tried so far?





