Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
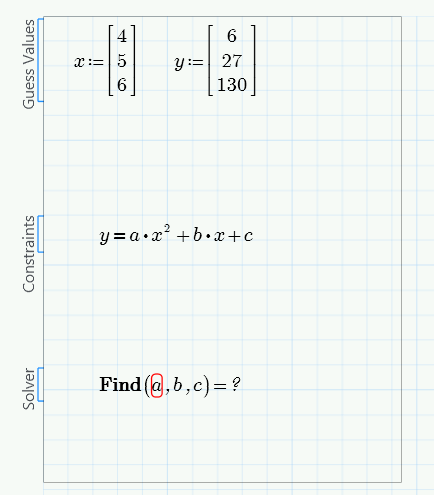
Getting coefficients of a quadratic equation based on three points
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Getting coefficients of a quadratic equation based on three points
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Provide some guess values for a, b and c.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Stuart, that looks like it worked.
But then the question follows: why does MathCad expect you to guess values for variables that we trying to solve for? Is that just for the sake of declaration? If that is the case, then it seems awkward, especially, since these values are arbitrary.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
David Aranovsky wrote:
Thanks Stuart, that looks like it worked.
Good. I checked it in Prime 1 after I posted and it worked as well.
But then the question follows: why does MathCad expect you to guess values for variables that we trying to solve for? Is that just for the sake of declaration? If that is the case, then it seems awkward, especially, since these values are arbitrary.
As Fred says, the numerical solvers generally require a starting point (guess values) - the solvers are fairly general and a number of problems have solutions that are dependent on the initial values.
Local minima and maxima are a good example - starting on side of the 'hill' or the other may take you to completely different minima. I posted a worksheet on the Hooke-Jeeves search algorithm here: http://communities.ptc.com/message/185455#185455 . It contains an example near the bottom of what happens when you specify different initial values.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Generally Mathcad wants a starting guess at the answer so it can launch its' numeric solver. You put x and y in for guess values, try assigning guesses for a, b, and c.
Attached is your problem solved in 14/15, I don't know if it will convert to Prime.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Fred!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is actually a set of linear equations in the unknowns, so here are a couple of ways of solving them without the need for initial guesses:
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Alan!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator