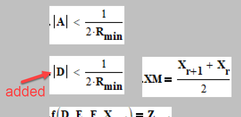Given/find works fine outside but does not work within a loop

[adnn]

Hello everyone,

Would really appreciate your help in an issue that I'm facing (in Mathcad 15)

I'm trying to fit two curves (parabolas) between two points (could be more later) and certain conditions (slope = 0 at so-so point). 

The given/find equation seems to work fine, but I am not able to loop through it.
The mathcad file is attached. Please allow me to quickly explain what I intend to do
1) I'm defining two parabola as y(x) = Ax^2 + Bx + C and y(x) = Dx^2 + Ex + F

2) Parabola 1 passes through point (x0,y0), with slope = 0
3) Parabola 2 passes through point (x1,y1) with slope = 0
4) They must meet at some point in between (XM,ZM) with the same slopes 

Lastly I find the unknown variables (A,B,C,XM,ZM,D,E,F) and store them in a 8x1 matrix.

But if I need to loop through n points, then I would like to use the same given/find in a loop and store all the calculated uknowns (A,B,C,XM,ZM,D,E,F) in an 8xn matrix. Here I get the error "this variable is undefined" and I have absolutely no idea where I am going wrong.

Many thanks in advance,

Warm Regards,

Aravind.

[Werner_E]

A solve block is not supposed to work within a program.

But you can turn a solve block into a function dependent on the variables you'd like to vary and call that function within a program.

Simply close the solve bock with something like

fun(x,y,z,..):=Find(....)

without an "=" at the end!

x,y,z are the variables you'd like to vary .

[Werner_E]

See if the attached helps. I made the solve block function dependent on the row index r.

BTW, you should consider using units in your sheet! After all you are using Mathcad and being able to deal with units is a big advantage.

[adnn]

Thanks for the timely help. Your sheet works perfectly  but I am not able to understand why.

I was wondering how you were able to call the fun function (which does the find) multiple times without defining the constraints each time (Given block is defined just once at the top, that too not with global definitions (ctrl + ~)) 

Since mathcad follows a top-down approach, it processes the Given, and then after the loop runs first time, it's done processing a find. For the next loop, how does it know the given conditions ?

Edit: I completely agree with the units (mathcad's the best at it). But since my sheet is dealing with pure geometry and there is just one unit (metre) throughout the sheet, I skipped the units for now, but will definitely add them once the sheet is working completely.

[Werner_E · Accepted solution]

> I was wondering how you were able to call the fun function (which does the find) multiple times without defining the constraints each time

The reason is that I turned the whole solve block into a function. So it can be called later over and over again just by using its name "fun".

But be aware that every call uses all the value, guess values, vector I, R.min, etc. with the values they had when the solve block was defined.

If you, lets say, change the value of R.min after the solve block function is defined, this has no effect on the outcome of a call to "fun".

If you would like the solve block function to use different values for R.min at every call, you would have to make R.min an argument of the function, too, alongside with r.

You may even provide different guess values that way if you make a guess value a function argument. You may then delete its definition above the solve if you do so.

BTW, you should be very careful with global assignments and use them rather sparingly.

Another thing I just noticed: You had defined function f, f' f" twice which is unnecessary. The name of the formal arguments do not matter. You may define f(a,b,c,x):=... and use it later with f(D,E,F,X3)=... as a constraint.

And when you define ff and gg for plotting, you may write ff(x):=f(A,B,C,x) and gg(x):=(D,E,F,x). Less failure prone than repeating typing the same function term over and over again.

[adnn]

Thanks a lot for the detailed explanation Werner !

Thank you for the insightful comments too (The sheet works just fine even without the other function defined, as you pointed out). I defined some variables globally just because I could (trying out new things :)) I'll change it to normal assignments.

[Werner_E]

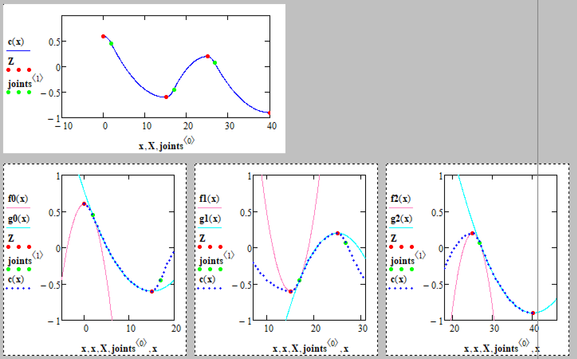
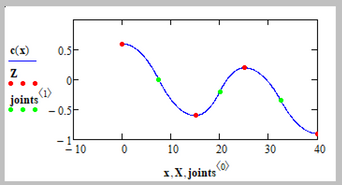
Just for fun I tried to plot the whole cable and I think theres a problem.

The point of joint (XM/ZM) is not always inbetween X[r and X[r+1.

All constraints are fulfilled, but I guess the result is not what you are looking for.

Adding X[r < XM < X[r+1 as an additional constraint makes the solve block fail for some values because it is not able to find a solution.

Maybe using different guess values for different situations can help.

Let me know what you think.

Maybe I can give it a try later

[adnn]

Yes, I also think this is far from a completely working solution. But the biggest obstacle is over. 

Some minor tweaking has to done (as you pointed out, XM has to lie between X[r and X[r+1), in addition, since one parabola is convex and the other is concave, so A and D will have to be opposite signs. In addition, I am also working on changing Rad[min at different points. This will take some time I guess :D.

 
Also, it is often not possible to plot curves which are too steep, so a solution is not always guaranteed. So if the solve function fails, the coordinates X[r or Z[r will have to be manually adjusted (which is not an issue).

I wonder if mathcad can provide some help in that (excel vba has the very excellent "msgbox" command which can function both as a marvelous debugger and user interface). Ideally "on error -- break" equivalent command in the for loop will stop the function from running whenever solution is not reached, so user can find it out and start tweaking the relevant inputs (since he knows where the curve stopped to plot). I'll give it some tries and if it fails I always have this awesome community to help me out ! 😄

Thanks a lot for the help Werner, I'll be sure to keep you posted on the updates.

[Werner_E]

Here is a somewhat improved version.

I added X[r<XM<X[r+1 as constraint, got rid of the absolute value when you compare the two derivatives at XM (you won't be happy if they intersect at right angles because the slopes are +1 and -1, I guess) and I added a rudimentary way to provide different guesses for A and D depending on which of the two endpoints is higher. The latter is the reason why I implemented the solve block function as auxiliary function "fun_" which is called by "fun" with the correct guesses.

It seems to work so far but just to be on the safe side I threw in the "on error" command to return an 8x1 vector full of NaN's just in case the solve block might fail.

You may add R[min to "fun_" (and maybe also "fun") as additional argument. What will R[min be dependent on?

So far it looks quite good, I guess:

[Werner_E]

Oh man, looks like I must have too much spare time. Sure should get some life.

I played around with the sheet and noticed, that the point of joint always is very near to the first of the two endpoints. This seems to be because there still is one degree of freedom in your system because |A|=1/(2R) looks like it rather should be |A|<1/(2R).

After changing that I added a constraint and demanded that XM should be right in the middle of X[r and X[r+1. It worked.

If you experience problems you might consider adding a lighter constraint like 2X[r + X[r+1 < 3 XM < X[r + 2 X[r+1  which forces XM to somewhere in the center third.

One other idea: if you add more constraints and experience the problem that the solve block does not find a solution, you might consider replacing "find" by "MinErr". If there is a solution Mathcad will find it but if there is no solution it will give you at least some kind of best fit as result.

[Werner_E]

Corrected version

Had the  "on error" statement at the wrong place.

Played around with randomly generated coordinates and use of "MinErr".

See annotations in the sheet,