Skip to main content
P
ptc-62076291-Visitor
1-Visitor
June 20, 2014
Solved

Having issue with solving in terms of another variable

  • June 20, 2014
  • 2 replies
  • 3266 views

I have attached what I have so far. At the bottom I have come to the point where I want to solve for x with a given Ka. I am stuck on this one.

Best answer by Werner_E

As for the check: Both solutions pass, but there is some numeric roundoff for the positive one. Not surprising if you consider the coefficients of your quadratic equations are in the range of 10^12, 10^13 and you provide just 12 or 13 decimals of the constant in the denominator.

Generally numeric evaluation (as opposed to symbolic one) is limited to 16-17 decimals anyway.

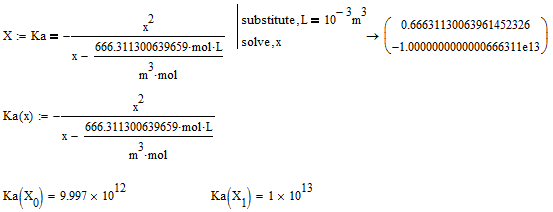
20.06.png

2 replies

M
MikeArmstrong1-Visitor
1-Visitor
June 20, 2014

Like the attached using a simple Given/Find solve block?

P
ptc-62076291-VisitorAuthor
1-Visitor
June 20, 2014

Not quite, I am looking to either solve symbolically for x= something in terms of Ka, or for actual answer of x. The last two equations on your page get off track somehow. I also find it hard to believe that x is a negative number. I don't think it is solving correctly.

M
MikeArmstrong1-Visitor
1-Visitor
June 20, 2014

The formula does return a positive and negative value for x.

Attached is a symbolic solution which returns the same answer as Werner.

Note I have remove the empirical unit handling.

W
Werner_E25-Diamond I
25-Diamond I
June 20, 2014

Does the attached sheet help?

P
ptc-62076291-VisitorAuthor
1-Visitor
June 20, 2014

Im really not quite sure what is going on in that sheet. I am a beginner and I think this is probably a bit easier than what that looks like. Here is what it can really simplify down to. The only two variables are Ka and x, the other things are just units. I want to solve for x.

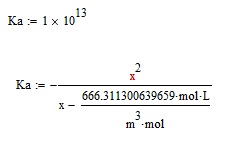
mathcadex.jpg

W
Werner_E25-Diamond I
25-Diamond I
June 20, 2014

Its basically a quadratic equation you want to solve. So there are two solution - given the value of Ka you supplied, one solution for x is negative around -10^13, the other is positive (around 0.666).

I used the symbolic solve and because I assumed you would be interested in the positive solution, I used the command assume, x>0 to omit the negative solution. If you delete this assume statement, you get both solutions in a 2x1 vector - give it try.

I also used the variable M in the equation instead of the copied value - hope thats what you intended.

In fact I first tried to use a solve block like Mike has done, but I wasn't able to find a guess value which would yield the positive solution.

There is a big drawback in using the symbolic solver - it doesn't know anything about units and sees m, L and mol as unknown variables. Its able to cancel mol, but not m^3 and L. Thats why I told the symbolic solver to substitute L by 10^-3 m^3. That way all units can be cancelled and we get the scalar solution as expected.

As you demanded also a symbolic solution, you either have to solve before you define Ka or make Ka unknown to the symbolics by writing Ka:=Ka.

Here you are - the symbolic solution, followed by both solution in their numeric representation:

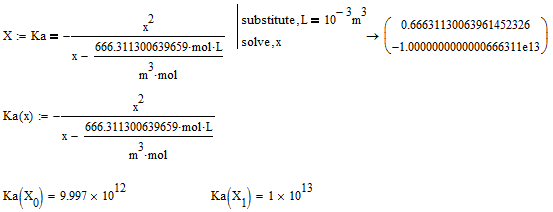
20.06.png

Terms & ConditionsCookie settingsAccessibility statement