We are aware of an issue causing pages to load incorrectly for some users and expect a fix soon. Sorry for the inconvenience.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Heat transfer between pipeline and aluminium anode sub-sea
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Heat transfer between pipeline and aluminium anode sub-sea
I am struggling to find where I am going wrong in the attached mathcad sheet. I have a pipeline with an internal fluid of 82.2c and then a thin coating then a 50mm thick aluminium anode is clamped around the pipeline (details on sheet). The sea temp is 5C but I keeep getting the external aluminium surface at the same temp as the sea water.
Before there is no hair left on my head where am I going wrong?
John
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Middleton wrote:
Hi Lou,
OK I see what you are saying but how do insert a thermal resistance between the aluminium and sea-water?
Many thanks,
John
Sorry comments is in Russian
http://twtmas.mpei.ac.ru/mas/worksheets/therm/Heat_Flow_4.mcd
but see the picture in the WebSheet
>how do insert a thermal resistance between the aluminium and sea-water
You can use ) know alpha2 (heat transfer coefficient - W/(m^2 K)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Middleton wrote:
I am struggling to find where I am going wrong in the attached mathcad sheet. I have a pipeline with an internal fluid of 82.2c and then a thin coating then a 50mm thick aluminium anode is clamped around the pipeline (details on sheet). The sea temp is 5C but I keeep getting the external aluminium surface at the same temp as the sea water.
Before there is no hair left on my head where am I going wrong?
John
1) It will be good to have a picture of your pipe - as here for example
2) May be this help you
3) See the attach too
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Thanks very much for replying. I am struggling a bit to follow it as my Russian is not that great. Can you explain a little more if possible in English for me?
Thanks in Advance
John
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Middleton wrote:
Hi,
Thanks very much for replying. I am struggling a bit to follow it as my Russian is not that great. Can you explain a little more if possible in English for me?
Thanks in Advance
John
Sorry, I try use both languages on my Mathcad Serve.
It is one page from the Web Reference Book Power & Heat engineering:
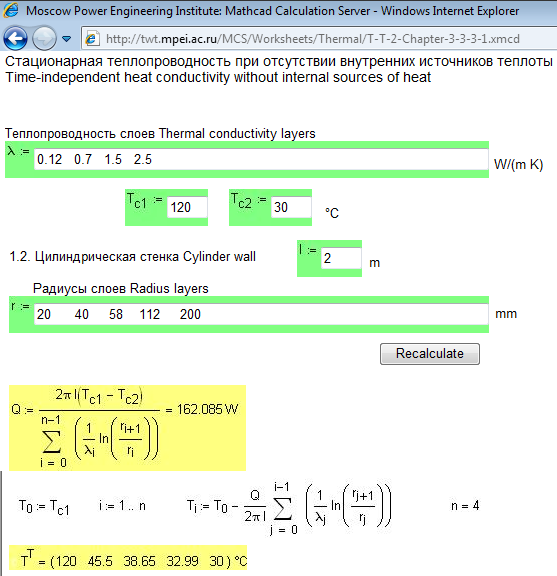
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
I have atatched the file thermal gradient3 filled in as you suggested.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Middleton wrote:
Hi Valery,
I have atatched the file thermal gradient3 filled in as you suggested.
Thanks, John!
Now I see your task.
You have temperature of a fluid in the tube and temperature of sea water and want to calculate temperatures in the multislide tube.
But you must know conditions of heat transfer from a fluid in the tube to the tube (in. surface - alpha1) and from the tube to sea water ((out. surface - alpha2).
It is a heat transfer task of 2-d kind.
See again http://twtmas.mpei.ac.ru/mas/worksheets/therm/Heat_Flow_4.mcd
There are a lot of formulas for calculate alpha1 and alpha2
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The unit C is a Coulomb. Temperature units in Mathcad have to be handled in a special way. See "Help", "Tutorials", "Features in Depth", ""Temperature and User Defined Units".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
The unit C is a Coulomb. Temperature units in Mathcad have to be handled in a special way. See "Help", "Tutorials", "Features in Depth", ""Temperature and User Defined Units".
Sorry, with units all is Ok!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, with units all is Ok!
Interesting. And a little worrying. I looked, and it was just "C". Then about 3 minutes later my computer blue-screened on me! Now it shows the correct temperature units!
Time to back everything up!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why would you expect something else? Not withstanding Richard's comments on units, you have set up the problem as a heat flow calc between two defined temperatures, t1 and t5, with three intervening thermal resistances in series. The assumptions of the calc are that the inside temp is t1 and the outer anode temp = sea temp= t5; the basis of your calc. Getting Tanode at exterior = Tsea=t5 is just validating the assumptions of your calc. Is there some other resistance you expect that is not in the model?
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Lou,
T5 is the sea water temp and T4 is the anode surface temp. The anode outer temp (T4) isn't assumed to be the same as the seawater temp. Does that give it a bit more clarity?
Thanks
John
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Middleton wrote:
Hi Lou,
T5 is the sea water temp and T4 is the anode surface temp. The anode outer temp (T4) isn't assumed to be the same as the seawater temp. Does that give it a bit more clarity?
Thanks
John
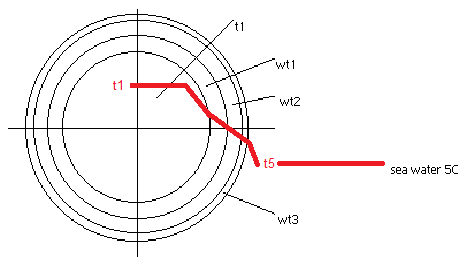
John!
Please create the picture with r1, r2... T1, T2... using a template in my attached file!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
" T5 is the sea water temp and T4 is the anode surface temp. The anode outer temp (T4) isn't assumed to be the same as the seawater temp. Does that give it a bit more clarity?"
I think you are assuming that T4=T5, since there is no thermal resistance defined between the outer anode surface and sea water which can allow for any temperature difference between the two. The overall delta T in the calc is T1-T5 (interior to sea water). this is split among three thermal R's, the outside of which is the anode. Implicit in the heat calc (Q=dT/R) is that the outer anode temp = sea water temp.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Lou,
OK I see what you are saying but how do insert a thermal resistance between the aluminium and sea-water?
Many thanks,
John
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Middleton wrote:
Hi Lou,
OK I see what you are saying but how do insert a thermal resistance between the aluminium and sea-water?
Many thanks,
John
Look up film coefficients in fluid heat transfer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Middleton wrote:
Hi Lou,
OK I see what you are saying but how do insert a thermal resistance between the aluminium and sea-water?
Many thanks,
John
Sorry comments is in Russian
http://twtmas.mpei.ac.ru/mas/worksheets/therm/Heat_Flow_4.mcd
but see the picture in the WebSheet
>how do insert a thermal resistance between the aluminium and sea-water
You can use ) know alpha2 (heat transfer coefficient - W/(m^2 K)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
Thank-you for your help it is very much appreciated. At least I get to keep my remaining hair!
Cheers,
John
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Middleton wrote:
Hi Valery,
Thank-you for your help it is very much appreciated. At least I get to keep my remaining hair!
Cheers,
John
I am glad to help you.
See about alpha or h (heat transfer coeff.) here http://en.wikipedia.org/wiki/Heat_transfer_coefficient
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If the sea water is not considered an isothermal medium, then the model must allow for this. The simple calc attached shows that the temp drop in the water itself is significant.
For the simplified infinite cylindrical model assumed in the calc (althought there's an L = 120mm with a dia of ~ 1meter, the L is not srelevant to the calc), we can assume that the sea water adds another cylindrical layer outside the solid pipe, with the conductivity of sea water, and that the water temperature is t5 (5degC) outside this water "tube." Not completely realistic, but good enough to look at relative temperature drops. This also ignores any efect of convection/currents.
Since the water conductivity is relatively low compared to the metal pipe, and the effective thickness can be large compared to pie thickness, the effect of the water thermal R is not negligible. Allowing for just 100mm additional thickness of a water tube about the pipe make the overall resistance about 6x higher, makes the net power flow smaller by this factor, and results in most of the temp drop (approx 5/6 x 77deg = 64deg) being across the water cylinder, leaving the outer surface of the anode at ~ 69 = 82-13 deg). Increasing the effective water tube thickness makes the temp difference across the pipe even smaller. Allowing for 1m water tube thickness results in only ~ 3degC temp delta across pie surfaces.
The water resistance grows logarithmically with thickness, and is slow, but nonconvergent; perhaps useful until the 2D model fails or other mechanisms, e.g., convection, come into play.
My conclusion from this is that the pipe model alone does not cover enough of the physically relevant situation to give meanigful results, and the model needs to be fixed before using its results.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Treating the salt water in the open sea as a conductor is not valid. Convection is probably the most significant heat transfer mechanism from a solid to a free fluid. The only time conduction would be more significant would be in a baffled construction where fluid motions were constrained; even in an open container convective currents would be created and play significantly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I agrre that the model used is the key to the analysis. If convection is dominant, then assuming the sea as an insothermal in contact with the outer pipe layer - the original anaysis - may be a reasonable assumption. I took the a simple, but not necessarily physically relevant, conduction model for sea water as a means to show that its conductivity has a significant effect on the calculated temp drops. Besides, it's the only one I know how to set up and analyze easily, and physical reality be damned :-).
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
If the boundary layer between the pipe wall and the sea particles have zero velocity then the heat transfer will be conduction not convection. Ouside this boundary convection would then become dominant?
I am only interested in the surface temperature of the aluminium and not concerned with any effect the surrounding sea may have outside this immediate boundary surface.
Thnaks,
John
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Middleton wrote:
Hi Fred,
If the boundary layer between the pipe wall and the sea particles have zero velocity then the heat transfer will be conduction not convection. Ouside this boundary convection would then become dominant?
I am only interested in the surface temperature of the aluminium and not concerned with any effect the surrounding sea may have outside this immediate boundary surface.
Thnaks,
John
The effective thermal boundary layer is the film of "film coefficient." How thick it is and how efficiently it transmits heat away from the aluminum will depend on the state of the sea outside the boundary layer. What you are describing is "free convection," where there is no driving effect to create an external flow in the fluid. This is not a simple calculation.
I've excerpted an equation from Marks' Standard Handbook for Mechanical Engineers, 7th ed for laminar film coeffficients, (pp4-100 to 4-104.) I can't (in a short time) get the units to balance, which is a standard problem with empirical equations.
Good Luck.





