Help and reality do not fit.

[gmunksgaard]

Error in getting the max dynamic value of corner post force origin from the containers stowed on hatch cover.

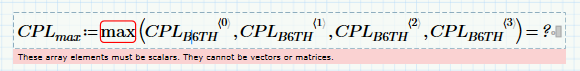
And according to the ”Help function” you can use Arrays?????? (the result of “IsArray” function is 1)

[-MFra-]

Hello Gert,

you should check that the matrices have all the same size.

[LucMeekes]

The four arguments are four columns of the same matrix, so they should be all vectors with the same length.

As an alternative try :

max(submatrix(CPL.B6TH,ORIGIN,ORIGIN+rows(CPL.B6TH)-1,ORIGIN,ORIGIN+3)).

It could be that each of the CPL.B6TH<x> is a nested matrix, in which case the max function fails:

Success!
Luc

[-MFra-]

In this case, just a small change, as follows:

[LucMeekes]

The question is what the OP wanted to determine the maximum of.

[Werner_E]

And according to the ”Help function” you can use Arrays??????

Yes, and thats true.

But what the help does not tell you is, that you have to use arrays of scalars.

In other words - the arrays must have elements which can be compared by size and they even can be complex numbers (which can't be compared by size from a mathematical point of view) as described in the help.

You don't show it but the elements of your matrix where you provide the columns of seem to be not scalars. Maybe the are matrices themselves or something else.

You would have to provide mor information about your matrix and about what maximum you are looking for.

In this case it would be better to create a discussion/question and not a document as you did here, as we could not offer attachments like a Mathcad file when we comment on a document.

Furthermore comments to a document don't let it bubble up the list of recent post and therefore often are overlooked.

[LucMeekes]

"complex numbers (which can't be compared by size from a mathematical point of view)".

I know at least two ways to compare complex numbers by size:

1. The funny way how Mathcad and Prime have implemented it (see description above).

2. Comparing by their 'length' where length(c)=sqrt(Re(c)^2+Im(c)^2).

[LucMeekes]

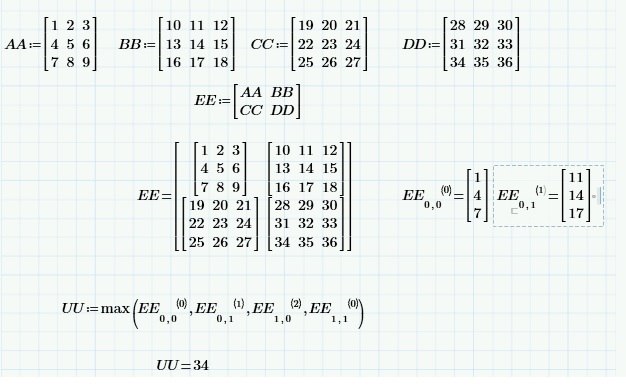
This is an other approach:

Luc

[-MFra-]

Would be fine if Gert would clarify some things. Or do we proceed by suppositions?

[vlehner]

Gerd,

maybe it helps you...

Volker