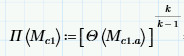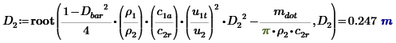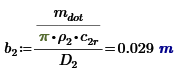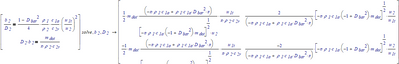Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Help regarding root function or find function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Help regarding root function or find function
I have the following equations and i am trying to ge the values for b2 and D2.
I have all the other necessary values but i cannot get to solve this.
Have i mistyped the root equation?
I tried with the find function too.
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
-
Mechanical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Some errors:
1. You've type rectangular brackets here:
(around the theta function). Don't ever do that unless you want to create a matrix.
2. Your equations are NOT unit balanced with the given guess values for b2 and D2, set them to be 1 m each to correct that.
3. The root function can solve only ONE variable, not two, and not an expression (like b2/D2)...
In this case you can pull a trick to solve it with root anyway: Multiply the first equation on both sides with D2^2, then the left hand segment becomes equal to the right-hand segment of the second, and we can solve for D2:
Now we know D2, we can solve b2 with:
Or you can look up how to use a solve block in Prime poperly, and use that.
Or you can solve the set symbolically, like I showed in my first reply.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please attach the Prime worksheet, not just a picture.
Success!
Luc
Apart from that, there appear to be two possible solutions:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Some errors:
1. You've type rectangular brackets here:
(around the theta function). Don't ever do that unless you want to create a matrix.
2. Your equations are NOT unit balanced with the given guess values for b2 and D2, set them to be 1 m each to correct that.
3. The root function can solve only ONE variable, not two, and not an expression (like b2/D2)...
In this case you can pull a trick to solve it with root anyway: Multiply the first equation on both sides with D2^2, then the left hand segment becomes equal to the right-hand segment of the second, and we can solve for D2:
Now we know D2, we can solve b2 with:
Or you can look up how to use a solve block in Prime poperly, and use that.
Or you can solve the set symbolically, like I showed in my first reply.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
for that equation, i used it like that because i received like that the formula with []. Thank you so much for the help!