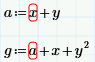Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to find a minimum of a chain of functions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to find a minimum of a chain of functions
Take the following 2 variables:
How do I use Mathcad to find the combination of x and y that minimizes g? Is it possible to do this while keeping a and g separate?
Please try to make a solution easy for a Mathcad newbie to understand
- Labels:
-
Mathcad Usage
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How do you insert that colored contour plot?
The textbox containing "Minimize(g,x,y)" doesn't seem to do anything. What is its purpose?
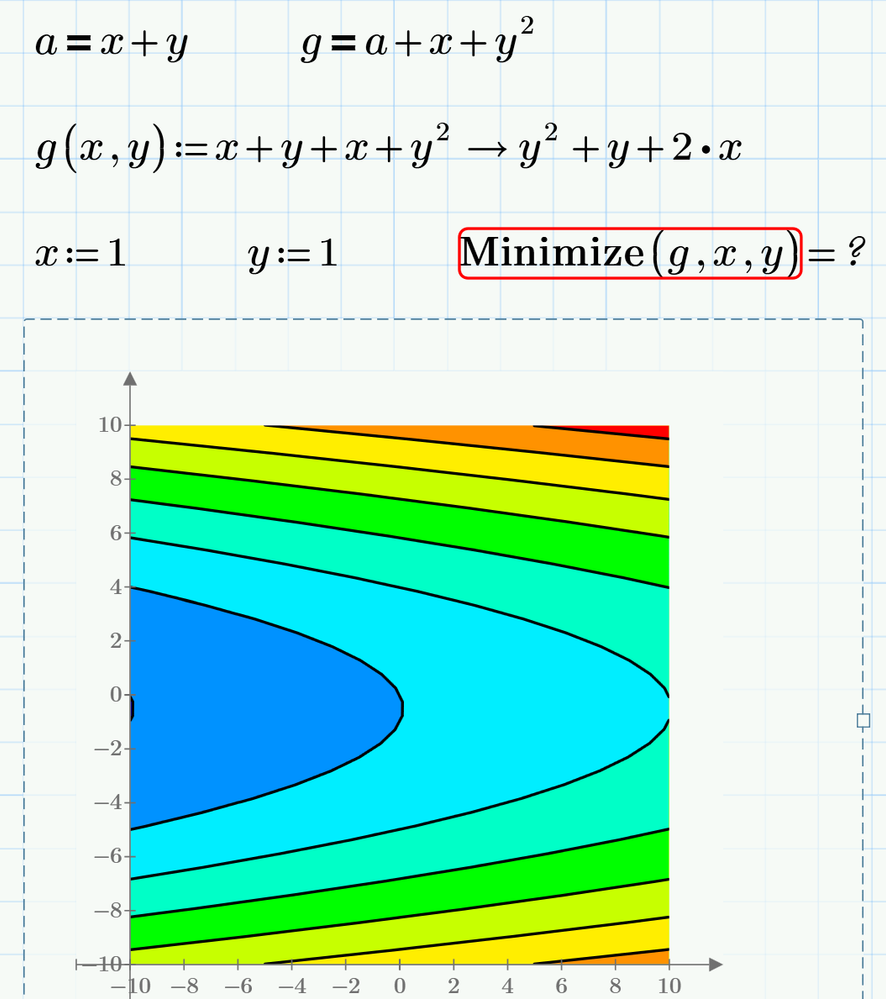
Could you generate the colored contour plot while keeping "a" and "g" separate?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1. How do you insert that colored contour plot?
On the ribbon, choose 'plots', then use the rightmost icon to insert a contour or 3D plot. See examples in the help info.
2. The textbox containing "Minimize(g,x,y)" doesn't seem to do anything. What is its purpose?
That isn't a text box, but an attempt to use the built-in Minimize function to find the minimum of the function, with guess values for x and y each 1. The function produces an error, indicated by the red box, because the minimum is reached for x= minus infinity.
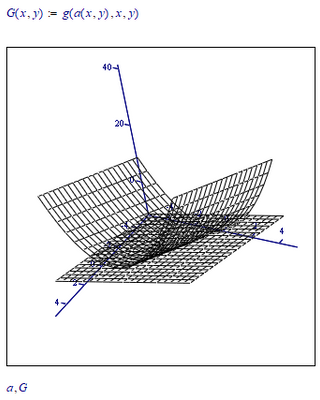
Here's another attempt:
Also fails, but with another function a :
3. Could you generate the colored contour plot while keeping "a" and "g" separate?
How would you like to keep a and g separate?
You could plot two surfaces as a function of x and y, one for a, the other for g (including a), is that what you want?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1. Thank you
2. Thank you
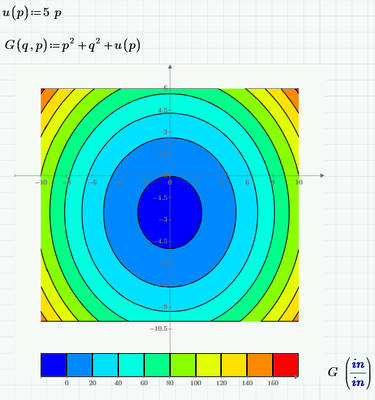
3. I figured it out. I wanted to use an equation in another equation and find the combination of 2 variables that would result in a minimum. This would save horizontal page space for very long equations. Something like this is what is exactly what I wanted to do:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc already explained why there can't be a solution if x and y are unconstrained.
In case you have additional constraints (like x and y being non-negative), you may use a solve block:
I guess the solution to "keep a and g separate" is to turn both into functions of x and y, right?