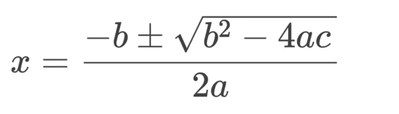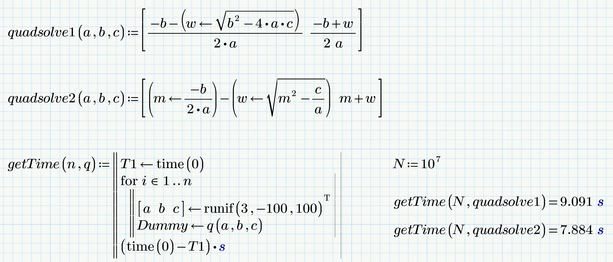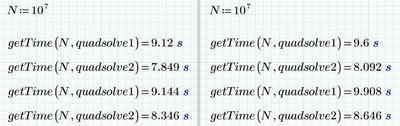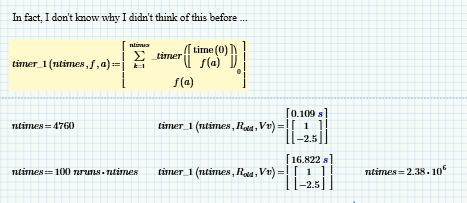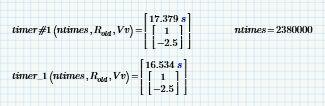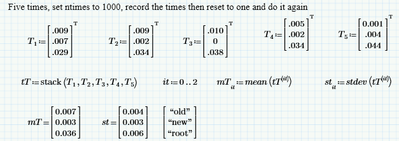Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How much more efficient is this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How much more efficient is this?
Apparently, https://www.poshenloh.com/quadraticdetail/ shows a 'new" way of solving quadratic equations.
It is described as "computationally-efficient, .."
Math Genius Has Devised a Wildly Simple New Way to Solve Quadratic Equations (sciencealert.com)
Does anyone know how to do timing tests in mathcad to check the difference in speeds in the "new" and the generally old method?
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Of course its just a different way to write the old well known formula and so you should not expect much difference in execution time - it mostly depends on the implementation (and also on the implementation of, e.g. the root function etc.).
Here's my comparison:
Here are a few more runs
Prime 6 worksheet attached, sorry, not working in Express
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A not very exact way is to use the "time" function inside of a program which calls the solvefunctions you created multiple times.
Components for a more precise timing were posted here a long time ago, but they won't work in Prime.
Did you already turn the "new" solve method into a Mathcad function?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No - I'll stick to the old. Fast enough for me.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E wrote:
A not very exact way is to use the "time" function inside of a program which calls the solvefunctions you created multiple times.
Components for a more precise timing were posted here a long time ago, but they won't work in Prime.
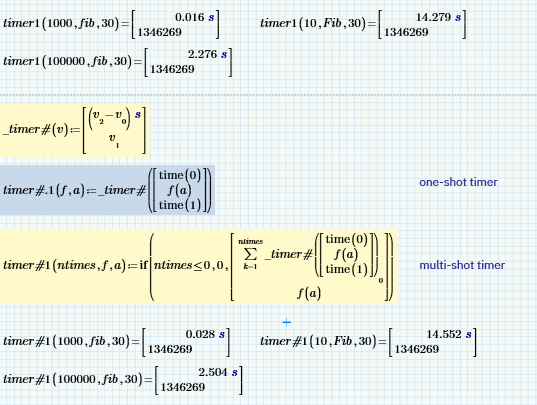
Here's a set of Very Approximate timing functions that will work in Mathcad Express 7. As you can see they're defined recursively (a seeming necessity in Mathcad Express) and have the usual recursion depth limit of about 4500 for n (the number of times to execute a function).
Needless to say, they could be converted to a program or redefined using a binary divide-and-conquer strategy for dealing with larger values of n.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think the argument is about computational speed, but more about not having to remind a formula.
You still have to calculate one square root and do some additions, subtractions, multiplications and divisions. But to save you from reminding that formula, you now have to remember a multi step approach, and it all comes down to the same (which is good, because you wouldn't want this new approach to find different roots for the same expression).
I don't know what is more complicated.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Of course its just a different way to write the old well known formula and so you should not expect much difference in execution time - it mostly depends on the implementation (and also on the implementation of, e.g. the root function etc.).
Here's my comparison:
Here are a few more runs
Prime 6 worksheet attached, sorry, not working in Express
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime 4.0 Express file attached. Try it!
We have a winner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
If you change that 1 as the first argument to timer1 to something like 10^3 or 10^4, you might get a better idea of the difference. The timer functions accumulate the time taken to execute function f n times.
Stuart
I'm away from a Mathcad machine at the moment ... I'm busy on my iMac, trying to get an Adafruit Feather RP2040 to do something and it's not cooperating! 👿
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
Taking advantage of Stuart's efforts:
Now I'm back at one of my Mathcad PCs, I could run your worksheet with larger values of n.
However, that cheat led to one of my many "Doh!" moments ...
Updated Mathcad Express 7 Timer worksheet attached.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Question:
When you raise the number of evaluations, are you counting the time of executing the function, or counting the time of executing the recursion?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
Question:
When you raise the number of evaluations, are you counting the time of executing the function, or counting the time of executing the recursion?
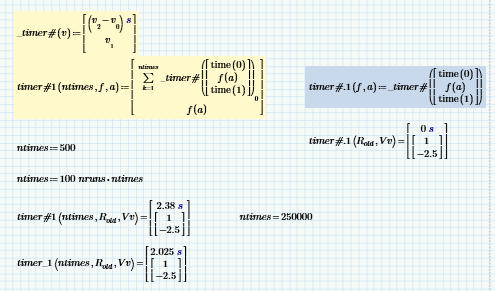
I'm reasonably sure that the recursion doesn't add to the total time, What will add to the total time is the cost of each call to _timer. The sequence of events at each iteration should be: call to time(0), call to f(a,b,c) {the thing being timed}, call to _timer {which involves packaging up time(0)'s result and f(a,b,c), then saving appropriate states to the stack and calling _timer. _timer then calls time(0) again and subtracts the first timer result from it to get the interval. At that point, anything else is irrelevant to the timing.
But, and this is a big "but", I don't know what either Mathcad or Windows is doing in between, or even during, each event. I note, for example, that there is often a huge difference between the time reported by my timers and the difference between "start" and "stop" when I use a watch to time things.
Using the summation operator got rid of the recursion limit, but should not, in principle, have had much effect on function timing.
As can be seen, the time is comprised of more than just the execution time of the function under test. However, I can't think of an "Express" way to reduce the processing overhead ... unless, 🤔 ...
... I incorporate the end time into the call to _timer:
The first time I tried it with the original ntimes, I got an error, but that seems to have gone away.
I'm not getting the impression that it gives improved (ie, shorter) times though, despite having taken the call to _timer# out of the loop. Here's the Fibonacci example from my timer worksheet:
Stuart
You'll have to stop asking me questions, Fred. Every time you do I start this "thinking" nonsense and it can't be good for me because it makes my brain hurt, and then it curls up under the sheets and want me to ask the bad man to go away. 🤕
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
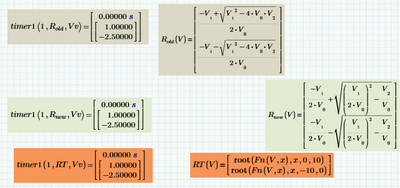
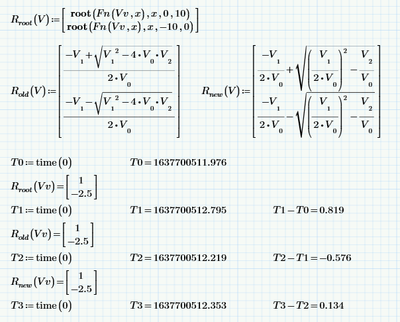
I guess the old method won:
It beat the new method by more than 0.7 seconds, and the root by about twice as much.
Or was that a false start?
(It appears that Prime does not calculate the sheet from left to right, top to bottom.)
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime is supposed to compute like old Mathcad did--top down left to right. You can check by moving evaluations relative to declarations.
But I'm not sure timing is working. I took my sheet and Stuart's suggestion to cycle multiple times to raise the interval. I selected (arbitrarily) 1000 cycles, and got:
Just for laughs, I reset by doing one time:


which is WAY more variance than I would have expected.
File (P4 express) attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
Prime is supposed to compute like old Mathcad did--top down left to right. You can check by moving evaluations relative to declarations.
But I'm not sure timing is working. I took my sheet and Stuart's suggestion to cycle multiple times to raise the interval. I selected (arbitrarily) 1000 cycles, and got:
Just for laughs, I reset by doing one time:
and did it again at 1000:
and was astounded at the difference. Five individual trials resulted in:
which is WAY more variance than I would have expected.
File (P4 express) attached.
Yes, Fred, there's can be a huge amount of variance in the times, which is probably due to everything that both Mathcad and Windows are doing in the background whilst Mathcad is evaluating the functions.
And that's why I caveated the timing functions by saying the results should be taken with a huge pinch of sodium chloride. However, they appear to be good for order-of-magnitude, wet-finger estimates, and will show significant variations in timings (as shown by my two Fibonacci functions).
It's nice to see the variance documented, though.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
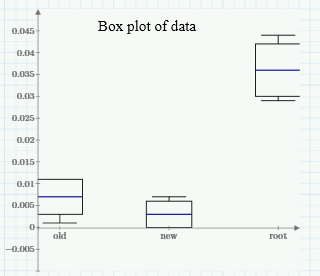
Boxplot of data from previous post! (I'm excited: I figured out Express could do boxplots!!)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
I guess the old method won:
It beat the new method by more than 0.7 seconds, and the root by about twice as much.
Or was that a false start?
Luc
I think you have to be wary of independent times, Luc. A lot appears to be going on between each evaluation, and that can (does!) affect the results from time.
(It appears that Prime does not calculate the sheet from left to right, top to bottom.)
If you reevaluate the worksheet, those negative times should go away.
Slightly reordered version of your results.
Also note the execution time obtained by putting the timers and the function into an array, thus limiting external events contributing to time differences.
Amended to remove the times taken to display the Tn times and to store the end times before calculating the time difference.
Those execution times seems consistently reduced compared to the originals when I've recalculated the worksheet.
Stuart
(Above results obtained using Mathcad Express 7)