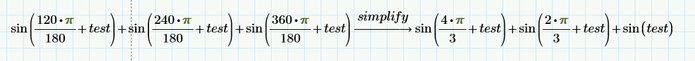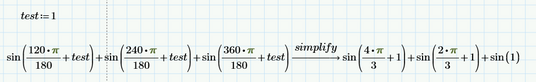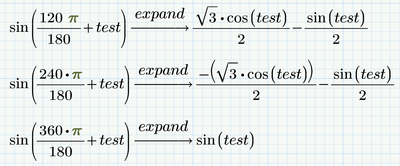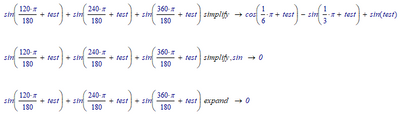Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Problems with simplifying expressions in Prime 7.0.0.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Problems with simplifying expressions in Prime 7.0.0.0
Hello all,
several days ago, I've updated my MathCad version to Prime 7.0.0.0.
However, now I'm facing problems with my old scripts as it seems that the new version is not able to simplify as good as the old version.
For example:
Obviously, the equation is 0 if test is a real number.
Also, the equation was simplified to 0 in the old version.
Even if I set test = 1, it is not simplified:
Is there any possibility to improve this new behavior?
Or is a different semantic required in the new version?
Thanks in advance and best regards!
Solved! Go to Solution.
- Labels:
-
Electrical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess you did not update from Prime 6 to Prime 7 but from a version before 6.
In Prime 6 PTC introduced a new symbolic engine as the default one, but we could still switch to the former, legacy one (MuPad). Starting from Prime 7 that older engine is not included anymore.
So I guess you have to live with the different results for now or try combinations of modifieres to get close to what you would like to see (the output of symbolic evaluations never was easy to control). Here in the forum you will find quite often complaints about the quality of the new engine even though in some rare cases the results of the new one are better usable compared to those of MuPad. I hope that PTC is scanning this forum, listening to its customers and working to improve the new engine - after all they have now full control over it, which was not the case with the former engine (it was licensed from Mathworks).
EDIT: I just played around with your expression and tried "assume, test=real", "simplify,max", "factor" to no avail.
BUT ... when you use "expand" instead of "simplify", even the new symbolic engine is able to simplify the expression to zero:
Don't ask me me "why" Prime can't find that most simply results on its own or for a logic behind it - its unfortunately just a matter of playing around and trial and error.
The reason why it works seems to be because "expand" in first place expands every single summand and as you can see below even a child can see now that the sum is zero:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I can't see the point in showing that the result is zero for just one specific value of theta and that Prime can show it numerically and symbolically.
MR_9862891 knows that the result is zero for any real value of test or theta in your post.
The problem is, that the new symbolic does not simplify to zero as it should and as the old engine did without problems and hesitation.
At least not when you use "simplify". As I had shown in my answer using "expand" does the job in this case. But thats not really satisfying as "simplify" should do the job as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Agree.
For the record, Mathcad 11:
But also:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess you did not update from Prime 6 to Prime 7 but from a version before 6.
In Prime 6 PTC introduced a new symbolic engine as the default one, but we could still switch to the former, legacy one (MuPad). Starting from Prime 7 that older engine is not included anymore.
So I guess you have to live with the different results for now or try combinations of modifieres to get close to what you would like to see (the output of symbolic evaluations never was easy to control). Here in the forum you will find quite often complaints about the quality of the new engine even though in some rare cases the results of the new one are better usable compared to those of MuPad. I hope that PTC is scanning this forum, listening to its customers and working to improve the new engine - after all they have now full control over it, which was not the case with the former engine (it was licensed from Mathworks).
EDIT: I just played around with your expression and tried "assume, test=real", "simplify,max", "factor" to no avail.
BUT ... when you use "expand" instead of "simplify", even the new symbolic engine is able to simplify the expression to zero:
Don't ask me me "why" Prime can't find that most simply results on its own or for a logic behind it - its unfortunately just a matter of playing around and trial and error.
The reason why it works seems to be because "expand" in first place expands every single summand and as you can see below even a child can see now that the sum is zero:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the fast and detailed answer!
I tried and it worked for the given example.
However, for my actual problem, I've again faced some issues.
By combining the expand and simplify commands ("expand,simplify"), however, the solver could also solve the more complex problem properly!
In my opinion, this is really an unsatisfying behavior of the new MathCAD version...
Actually, I'm only using MathCAD to analytically solve and simplify equations, because it is quite easy to handle and, in the past, it was usually able to solve all of my problems...
Again, thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To be easy to handle sure is one of the benefits of Mathcad (and even Prime), but for mainly symbolic calculations there sure are more powerful applications on the market (e.g. Maple, Mathematica).
In the times of Mathcad 11 there was Maple under the hood for symbolic calculations and so Mathcads symbolics could be said to be state of the art. But beginning with Mathcad 14 the symbolic engine changed (to MuPad) and it could only be said thats its a nice-to-have and quite powerful for a software with the focus on numerical calculations, but it wasn't state of the art any more, although of course sufficient and powerful enough for many purposes.
The change to the new symbolics since Prime 6 looks like another step backward so far, but the hope is, however, that the new symbolics has the potential to be significantly improved. Future Prime versions will show whether this hope was justified.