Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to check each element of a matrix and to get the result depending on the conditions that are fulfiled
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to check each element of a matrix and to get the result depending on the conditions that are fulfiled
As you can see in the attached file, i have 2 matrices and i want to check a condition for each element and to show the result depending on the condition that is fulfilled. When i try the normal "if" condition it says that it has to be a scalar.. i know I have to access at each element but i dont know how.
Thanks in advance
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> Otherwise, the result must be 11x11
Otherwise?? I guessed the result should be a 11 x 11 matrix in any case. Some matrix elements will be 0 and some calculated based upon your two formulas.
>|M.xy| is only the absolute value of M.xy.
Thats what I suspected. And I guess the same is true for |M.x| and |M.y|, too.
So the best solution in my opinion would be to turn the calculations into functions and write those functions as if only normal scalars are involved. The names of the formal arguments do not matter, as you can see in my solution for m.x_top().
And if this function does what it should for single scalar values, you may then call it vectorized (!!) with your matrices as arguments to get the matrix you are looking for.
See if the attached solution helps and provides the correct results you expect:
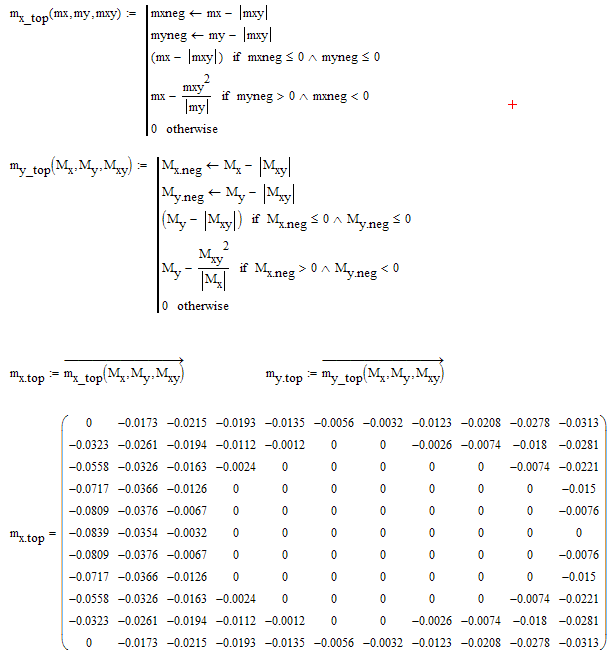
Regards
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think you must use for... for... and compare each element of both matrix.
Now you have a Boolean matrix not a scalar:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
but for M.x.neg<0 for instance i need to get the result M.x-|M.xy|.. (im talking for 1 element.. the other element of the matrix can be different, 0 for example if the other condition is fulfilled
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its not clear to me what you expect as result for m.x.top. Guess it should be a 11 x 11 matrix .
What do you intend |M.xy| and similar expressions to be?? The way you have done it in your sheet its the determinant of the full matrix M.xy, but maybe you want it just to be the absolute value of the single element in M.xy. Please clarify.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
but the condition M.x.neg<0 and M.y.neg<0 must be checked in all the matrix because some elements fulfill this condition some not. better to say the condition must be M.x.neg(i,j)<0 and M.y.neg(i,j)<0, with i and j being the element row and column. so for every element, the conditions must be checked and provide the result. Otherwise, the result must be 11x11
|M.xy| is only the absolute value of M.xy.
I will consider element 1,1 for example: for M.x.neg(1,1) we have Mx(1,1)-|Mxy(1,1)| and for M.x.neg(1,) we have My(1,1)-|Mxy(1,1)|. now for this element the condition is that IF M.x.neg(1,1)<0 and M.y.neg(1,)<0 the result for element 1,1 must be Mx(1,1)-|Mxy(1,1)|, if both are greater than zero than te result for element 1,1 must be 0. This way all 4 conditions must be checked for each element of the matrix.
The point is that i dont need the result to be any of the given matrixes, I want a new matrix where every element fulfills the condition.
Hope i am bein more clear now ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> Otherwise, the result must be 11x11
Otherwise?? I guessed the result should be a 11 x 11 matrix in any case. Some matrix elements will be 0 and some calculated based upon your two formulas.
>|M.xy| is only the absolute value of M.xy.
Thats what I suspected. And I guess the same is true for |M.x| and |M.y|, too.
So the best solution in my opinion would be to turn the calculations into functions and write those functions as if only normal scalars are involved. The names of the formal arguments do not matter, as you can see in my solution for m.x_top().
And if this function does what it should for single scalar values, you may then call it vectorized (!!) with your matrices as arguments to get the matrix you are looking for.
See if the attached solution helps and provides the correct results you expect:

Regards
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you





