Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to extract a symbolic only function to the numeric processor
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to extract a symbolic only function to the numeric processor
Some functions are only recognized by the symbolic processor. I am looking for a way to encapsulate some of these functions so they are available to the numeric processor via a normal function call. An example with one such function - Si(x) - is shown in the attachments, with various schemes I have tried. The element-by-element approach in item 2 works for assigning values to an array of arguments, but is a bit more awkward than I prefer. My attempts at defining a function in items 4-6 haven't worked.
Is there a way to define a function that is recognized by the numeric processor that does effectively what is in item 4, but works? If it can be done for a scalar, then I would assume that vectorizing this function would allow evaluation with array arguments, since the symbolic encapsulation is isolated in the scalar function definition.
If responding with a file, please save in mcd11 format.
Thanks,
Lou
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As you can see in the attached pdf the behaviour of your sheet is differently in Mathcad15 - we get an error in item 2.
Nevertheless I seem to have found a way to turn Si into a numeric function which at least works in Mathcad15, hopefully in Mathcad 11, too.
I have just played around with it and you can even make the precision (now fixed to 10) a second parameter of the function SiNum.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As you can see in the attached pdf the behaviour of your sheet is differently in Mathcad15 - we get an error in item 2.
Nevertheless I seem to have found a way to turn Si into a numeric function which at least works in Mathcad15, hopefully in Mathcad 11, too.
I have just played around with it and you can even make the precision (now fixed to 10) a second parameter of the function SiNum.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner - the paste of the full symbolic line into the program works as you suggested in mcd11. It then implements a scalar function. In mcd11, the vectorize is not implicit, as you show for Shi(v), but this is easy to resolve by modifying the program or just explicitly using vectorize.
While I have used symbolic manipulation and functions a fair amount, I have not created programs including them; they've been somewhat of a mystery to get working (as my attempts show). The help documentation wasn't helpful, as I expected, but I read through it anyway. Your hint about copying/pasting the full underlying symbolic line was key, and I expect to get my more complicated real work moving now that you pointed me in the right direction.
Thanks,
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Glad that it worked for you in Mathcad 11, too.
The copy and past thing is a real tricky one. I've learned it here (where else) when I was trying to write a program to solve a first order DE symbolically and no matter what the variable is named (should be a parameter of my function). While beeing quite tricky I succeeded but never tackled to expand to second order DEs since then.
You may even simplify SiNum by omitting the return line, BTW, making it a one-liner.
Its especially hard to see that the symbolic evaluation only affects the invokement of the Si-function an not the whole program/local assignment as you would get without copying.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Or still another simplification getting rid of he local assignment, too (the brackets are mandatory, though).

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In order to get rid of having to specify the number of digits for the numeric processor, while knowing that it can work with at maximum 17 digits, here is another simplification (works in MathCad 11), assign the result of the symbolic expression to any variable (here 'r' )
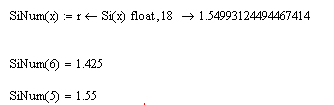
Now the numeric function behaves like a normal numeric function regarding formatting its results.
In defining the SiNum() function you have to first type the symbolic expression as:
Si(x)[CTL >]
then type the numeric function as:
SiNum(x):r{
then copy the symbolic expression and paste it into the placeholder of the numeric function definition. Done
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The point of the posting is to indicate that a precision of 18 is sufficiently (if you stick to numeric evaluations), right?
In my first post there was already a fixed precision of 10 (taken from Lou's original sheet). The precison as second parameter being meant as an option.
In your step by step explanation of how to retype my function you forgot about the float command - it won't work without. BTW, if you look at the last post of me which you answered at you can see that even the local variable is not necessary.
The behaviour concerning formatting seems to be different between Mathcad 11 and 15. In 15 I see the "full" precision (even more than 18 if specified in the function or via second parameter). So despite of using the numeric equal sign it seems to be somewhat seen as a symbolic result. Only if I verctorize (again) the normal numeric behaviour is seen. Strange and while its not important I do not understand, why.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the simp[le example I had given, there is no need to keep more precision in the symbolic result than the numeric processor can maintain, and there is no need to pass it as an argument, as you point out. In the real, more complicated case I'm working on, the symbolic expression to be evaluated is in fact a small difference of two quite large numbers. Here, the symbolic calculation must have high enough precision (~60-100) so that the relatively small difference is calculated accuratey. I may pass the symbolic precision as a parameter, or just leave it at the max of what I think I need. I do remember the many admonitions on the forum that the precision is the accuracy of all numbers in the symbolic calc, not the precision of the final result. Regardless, the normal numeric precision of this difference is then adequate for further work.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I do remember the many admonitions on the forum that the precision is the accuracy of all numbers in the symbolic calc, not the precision of the final result.
Yes. I keep pointing this out. The float keyword should be used very sparingly. And by that I mean almost never.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson schrieb:
I do remember the many admonitions on the forum that the precision is the accuracy of all numbers in the symbolic calc, not the precision of the final result.
Yes. I keep pointing this out. The float keyword should be used very sparingly. And by that I mean almost never.
This application seems to be one of the spare exceptions as it won't work without float.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This application seems to be one of the spare exceptions as it won't work without float.
Actually, in MC15 it doesn;t work even with it (it does work in MC11). I can't figure out how to make it work either.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson schrieb:
Actually, in MC15 it doesn;t work even with it (it does work in MC11). I can't figure out how to make it work either.
Interesting point. Obviously I hadn't tested enough. In fact I was happy when the "numeric" equal sign worked.
While I noticed that extended precision of the "numeric" result, I didn't pay the necessary attention.
Good for Lou that at least it works with MC11.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I may have started the celebration a bit early. The numeric functions can be defined and they appear to work correctly with no errors. However, my initial checks were with integer arguments, some of which gave very large values of the functions (which grow exponentially), and I confirmed that the difference of the two large terms is calculated corectly.
However...check out the attached sheet (with pdf also). When the arguments are given as real - with a decimal point - the precision is limited for the entire calc. I have no idea why, but this will put a damper on my ability to use the functional form. I may be able to salvage the calc by using integer values to validate a separate assymptotic approximation (good enough for engineering work), but the symbolic functions would need to work for real arguments in order to be useful.
RJ - I'm not sure why you used the symbolic equal at all after the initial fct def. Only the numeric assignment should be needed. See the xx vs. yy assignments.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
RJ - I'm not sure why you used the symbolic equal at all after the initial fct def. Only the numeric assignment should be needed. See the xx vs. yy assignments.
The behavior in MC15 and MC11 is very different. In fact, in MC15, with the MuPad symbolic engine, your differences work OK with floating point numbers.
If you pass integers to the symbolic processor (either Maple in MC11 or MuPad in MC15) the symbolic calculation is exact. If you pass floating point numbers the symbolic processor does arbitrary precision arithmetic. The default precision is 20, but the float keyword is supposed to change that. It seems that in MC11 it's not working correctly though, and the calculations are done using the default precision even if you try to increase the precision using the float keyword. Actually, I vaguely recall that there is an old thread about this problem, but I doubt I could find it now. Fortunately there is a solution to this problem, using a symbolic factor to convert the floating point number to the ratio of two integers. See the attached worksheet.
For those with MC15, don't worry. I have not gone completely mad. Factoring a floating point number has no effect using the MuPad processor (which is kind of annoying actually) ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For those with only MC15, here's what you get in MC11:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The factoring works for the direct symbolic evaluation with real numbers - except that it breaks when the argument is an integer with no decimal point. If a numeric function is defined, then it doesn't work with any integer, decimal point or not. For now, this is more an annoyance, since it easy to avoid exact integers in practical work. I haven't played with it enough (and may give up first) to see if there's a single workable form, or a conditonal in a program that can separate the integer (without using factor) and real (using factor) cases.
The attached files (v11 and pdf) shows how the symbolics simply don't evaluate in the integer case - very strange.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In MC15 it workes even in the integer case but as Richrad pointed out there are other problems.
As I have no Version 11 installed I can only guess: What if you follow the factor command immedeatly in the same eval by an expand? I guess expand would let the (necessary) fraction just created as it is but would reverse the factorisation of a pure integer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Try this. It uses symbolics enbedded in a program to always return an integer. It's a structure that cannot be created in any version post MC11, although it seems to work in MC15 (except that, as before, the precision shows it's really displaying a symbolic result, not a numeric one).

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This works when the function ReturnInt is separately defined, as in your example. I tried to incorporate the same functionality directly, but without success. Not sure how to make it work, but at this point, having the ability to do the symbolic-to-numeric calcs only for real, non-integer numbers (rather than only integers) is all that is needed for engineering work - with minor fudging to avoid integers.
In any case, I was able to use the ReturnInt function to validate some strictly numeric functional approximations to my desired accuracy, so I now have numerically defined functions to use without the need for symbolics at all.
Even if the ReturnInt/factor technique with symbolics is used, there are points to consider. One is that "factoring" arbitrary real numbers symbolically can result in numerator and/or denominator integers having many tens of digits. In practice, this number may need to be constrained, or at least considered when setting the float precision. E.g., if "factoring" results in a ratio of 20 digit integers, then the float precision may need to be increased by 20 digits - or more - in order to maintain the desired calculation precision. This is a bit unclear to me since I'm not sure how the symbolic calculation and float work in such cases.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This works when the function ReturnInt is separately defined, as in your example. I tried to incorporate the same functionality directly, but without success. Not sure how to make it work,
The numeric processor does not know what to do with the symbolic expression embedded in the program (it was never intended to be a valid construction, which is why it can only be created via a cut-and-paste loophole). So I think the only possibility is to incorporate it in such a way that only the symbolic processor sees it, as you did in the "test" function.
Even if the ReturnInt/factor technique with symbolics is used, there are points to consider. One is that "factoring" arbitrary real numbers symbolically can result in numerator and/or denominator integers having many tens of digits. In practice, this number may need to be constrained, or at least considered when setting the float precision. E.g., if "factoring" results in a ratio of 20 digit integers, then the float precision may need to be increased by 20 digits - or more - in order to maintain the desired calculation precision. This is a bit unclear to me since I'm not sure how the symbolic calculation and float work in such cases.
This is a good point, and I'm not sure how it works either. If the input expression contains only integers and you have no float keyword, then the symbolic processor does exact integer arithmetic and returns a result that contains only integers. So floating point precision is moot. But if you use the float keyword, and/or the input expression contains both integers and floats, I'm not sure when it converts the integers to floating point numbers. I would hope that it does exact arithmetic for every operation that does not contain a float, and then converts integers to floats only at the end. The fact that the ReturnInt function works implies that this is in fact how it works, but there is no way to be certain of that without a lot more work.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, bad news and some effects beyond my ability to explain.
BTW, Richard used the symbolic eval because in Mathcad 15 the expression to the left of "But it's not." throws the error "This value must be a scalar." which it obviously does not in Mathcad 11.
See attached the pdf which shows how Richard's file looks in MC15
Werner





