Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to find square root of a matrix
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to find square root of a matrix
How do you find the square of an each individual element of a matrix.
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Based on the title of the post, I assume you mean the square root of each individual element of a matrix.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Based on the title of the post, I assume you mean the square root of each individual element of a matrix.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thank you btw this only works for square matrixes.
mine isn't square.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
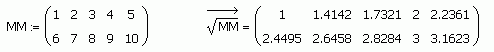
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It works for non-square matrices when I try it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here we go again ![]()
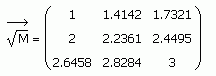
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I didn't bother trying that, because I assumed it would not work. I'm a little surprised it does!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not even sure why I tried it! ![]()
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ziyad,
Just a comment, in your prior posts I think you commend on the speed of the calculaitions.
In the Help, something like "features in depth", they talk about using the vectorize operation and it being slow, so if you are dealing with large matrices the program that Richard provided is recommended. In your prior posts the vectoirze operator is used a lot, it looks nice, but maybe to speed up you might want to replace some of the operations with a program.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the Help, something like "features in depth", they talk about using the vectorize operation and it being slow,
Are you sure? Vectorising is generally faster than an explicit loop. For this example, that is certainly the case.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
I havn't tested it, but please look at Quicksheets>Mathcad Techniques>Improving Calculation Speed.
If it is a natrual vectorization that is prgramed by Mathcad, it is fast, but using the vectorization operator, it is suppose to be slower.
Please let me know what you think.
Wayne
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
In looking at the artical again, maybe I read more into the last paragraph than I should have? Your test certanily suggestes that I did.
But, the test was for a small matirx problem done may times, What about avery large matrix done a few times, I think that is what the artical and (therefore) I was referring to. (How big is big)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
Sorry to keep bloviating,
I took your time funciton, and extended to allow for variable size square matrices
For small matrices, 8x8 and less, the vectorize method is faster. (an 8x8 is not very large)
For larger than 8x8, the program is faster.
For 50x50 size and larger, the program is twice as fast.
I attached the file and copied and pasted the results above on the right had side, so you can look at without having to wait.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its a fine balance, aesthetics vs time,
We're only talking about seconds here aren't we?
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Mike,
For smaller matrices and short worksheets, I agree, no real concern.
But for large matrices, operated on several times the difference can be measured in minutes.
If operating on very large data sets (ex., in my field, earthquake records), you need something else to do while the program runs. You need all the help you can get.
Just like memory allocation for matrices,
in a small worksheet, no concern.
with large matrices, a big deal, which leeds me to a question, on a separate thread.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
you need something else to do while the program runs.
Could always make a brew.... ![]()
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry to keep bloviating,
Hey, I just learned a new word! That's a great word, too. A week from now, all my friends are going to be sick of hearing it. ![]()
For small matrices, 8x8 and less, the vectorize method is faster. (an 8x8 is not very large) For larger than 8x8, the program is faster.
For 50x50 size and larger, the program is twice as fast.
Interesting observation! With a little more playing around it becomes apparent why. It seems that vectorizing matrices is a rather special case.
The Quicksheet only says that you shouldn't use vectorization when the function is implicitly vectorized already. It doesn't say that it is always a slow option. Unfortunately, it also doesn't explain that in many cases it is the fastest option, or what those cases are! So in the attached worksheet I have also tried to do a better job than the Quicksheet of explaining when to use vectorization and when not to use it.
Message was edited by: Richard Jackson - worksheet updated
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
Nice work, quick and well written.
But I was still concerned about large matrices, so I tinkered a little.
I have attached the modification, turned calculation off and cut and pasted the results at the end of the file, it takes about 7 min. to run.
This is what I did:
1) added a more complicated, though totally meaningless, function, matching the 5 types.
2) copied the functions and added preallocation for the X matrix, to compare effects of preallocation.
3) ran for square matrices for 10, 30, 40 and 50 rows (and columns)
Preallocation:
Only for the simple program and the 10x10 matrix, was the preallocation method worse than non allociation.
But for the more complicated function it is an imporvement and for the larger matrices, demonstrates that preallocation is very important, in fact for the column method, it is a factor of 3+ times faster.
So only comparing the Preallocation Methods:
For this case, the column and the element methods are compariable, with the column slighlty better.
The vectorized method is no longer competative above the 10x10 matrix.
So: For complicated and or large matrices, the program method with preallocation is always (well I think alwasy) better, and may be much better, that equations using the vectorize operator (as opposed to natrual vectorization).
Thanks in advance for your comments
Wayne
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Very interesting example! One can learn a lot from playing around with the various possibilities. Column by column operation is always the fastest, as long as you implement it right (which includes preallocation of arrays). See the attached for some comments. I also reduced the number of trials for each function so the worksheet runs in a reasonable time ![]()
I have also updated my worksheet earlier in the thread to include preallocation and to tack your example on to the end. The function versions in that worksheet are not quite the same as the ones in the worksheet attached to this post so you may also want to look at that.
Finally, note that there is a slightly easier way to preallocate: just run the loops backwards!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard:
Thanks much, I learn a lot looking at your work.
I am going to look at this over the next couple of days.
Just an observation:
As you say, the column option, if done in the most expedient way, appears to be the fastest. In looking at the results, the element by element is more or less the same as the other two column options.
The equation, I just pulled out of you know where, I was trying to make the vectorize option do more matirx operations and wasn't interested in simplifying, but maybe could have put a little more thought into it.
It seems the real advantage of the fourth equation is the use of the natural vectorization of the matrix squared. So it occurs to me that if I had an equation that did not have something like that to take advantage of, then all of the methods, exept the vectorize operator, should be about the same.
So I am thinking the real answer is that you should use the method that best takes advantage of any natural vectorization and use by column; but if there is no natural vectorization to take advantage of, then either by colunm or by element may be about the same. Would need to test speific cases.
In summation: The column method is the best method, except when it isn't; then its more or less the same as the element by element. Crap.
I ran a 150x150, just for the heck of it, but about the same.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems the real advantage of the fourth equation is the use of the natural vectorization of the matrix squared.
It also avoids the explicit vectorization of the cosine function.
So it occurs to me that if I had an equation that did not have something like that to take advantage of, then all of the methods, exept the vectorize operator, should be about the same.
If you remove that the column by column approach is still the fastest.
So I am thinking the real answer is that you should use the method that best takes advantage of any natural vectorization and use by column; but if there is no natural vectorization to take advantage of, then either by colunm or by element may be about the same.
Well, I can't prove it, but I suspect that column by column is never slower than element by element, and is usually faster.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ricahrd,
I agree with you on that.
I was actually thinking more generally about problems, programs, that may not be very amenable to operations with just column vectors; take advantave of the speed afforded by the natural vectorization in the program where possible, but after that, if other operations are done element by element and not by column operations, you are not necessarily paying a high price.
Perhaps you might start a new thread with your paper and a title that might attract others?
Thanks for your help
Wayne
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Perhaps you might start a new thread with your paper and a title that might attract others?
There's been discussion of a FAQ. I think perhaps "Forum Knowledgebase" would be a better name for it though. It could include a true FAQ as one document. That might be a good place to put something like this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fantastic explanation as usual.
PTC should add this to there quicksheets. Much easier to read and multiple examples as proof.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
my matrix will eventually blow up to 365 X 14, the loop will definitely help. Since i have to do lot of multiplications and divisions of these matrices.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ziyad,
The loop is not necessary the quickest way. Have a look at Richards worksheets. He proves that transposing the matrix and working through column by column is the quickest way followed by vectorization.
It does depend on the dimensions of the matrix, but Richard proves that looping through all the elements one at a time is not the optimum way.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike,
I don't think this is settled yet. When the matrices are preallocated, the results are very different.
I am hoping for a ruling from Commissioner Richard
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have you got an example?
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm really busy today, but I will look at ti.
You are correct that I shold have preallocated the arrays. I'll fix that. There are some issues with your functions, but I don't know how fixing them will affact the results until I do it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

Mike





