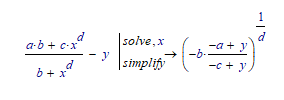Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to force Mupad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to force Mupad
First I want to apologize as I did send the same message 30 minutes ago but as I do not see it in the message list I am unsure whether it went through.
I would like to solve this equation (a*b+c*x^d)/(b+x^d)=y for x. In mathematica this went smoothly but not with Mupad (see worksheet). Could one of the more proficient Mupad users show me how I can force Mupad in giving me the same answer as mathematica?
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mupad? This forum is on Mathcad and Prime!
Anyway. It might help if you tell the symbolic processor what type of variables a...d and y are: If they're positive, and/or real (rather than complex).
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry Luc, I am using Mupad in Mathcad 15 (should have mentioned that).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No problem.
This is what Mathcad 11 with the Maple symbolic engine produces:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
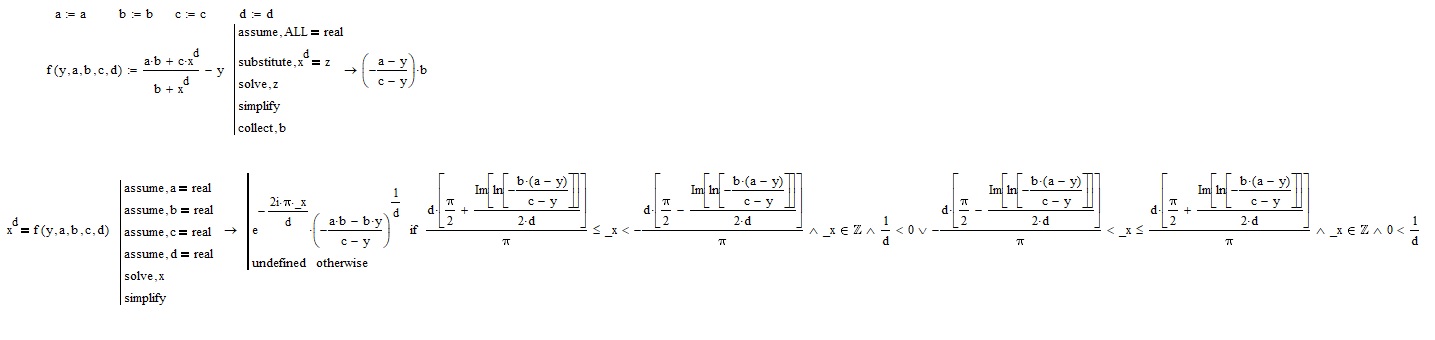
No surprise to me that MC11 with Maple solves it without issue (I am still missing my MC11 version). But is there any way I can obtain the same result with MC15? Adding simplify did not change much
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is not an answer, but it's as close as I could come:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The following study, using a simplified expression, may give you an idea of how muPad ticks. On contrary to Maple it defaults to domain complex and like the symbolics in older versions of Mathcad the assume modifier is not always achieving the desired effect.
Mupad seems to consider much more special cases in its calculations, it "knows" that powers are not defined in real domain for every combination of base and exponent, etc. and while this may be correct from a mathematical point of view it can be annoying in everyday use.
Maybe the problem is, that MuPad first was developed by university mathematicians. maybe the problem is, that Mathcad and Prime are using a very old and limited version of muPad. As muPad now is owned by Mathworks, owners of MatLab and a competitor of PTC (really? can we still say that Mathcad Prime is a competitor of MatLab?) chances are low that symbolics in Prime will be enhanced in the near future.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This was as closest as I could come with your equation:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you all for your help! All explanations were much appreciated