Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to re-code a Rkadapt() optimization problem using Odesolve block
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to re-code a Rkadapt() optimization problem using Odesolve block
in the book chemical kinetics with mathcad and maple, Figure 4.22 illustrates a very useful and interesting method to answer a reversible kinetic question,
after reading this example, I wanna rewrite it, for I think that Odesolve block is easier to read than Rkadapt() function. But during the recoding , I found that I
must change k to k(t), but this would not bring too much trouble during solving the ODEs. the problem arised during optimization, see the figure
Solved! Go to Solution.
- Labels:
-
Chemical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
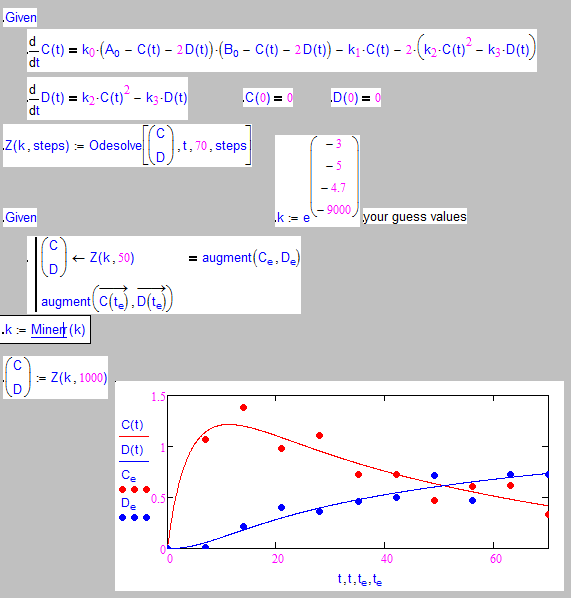
Is it something like this you are after?
I have changed your single scalars ki to a vector for compactness.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why did you change the constants ki to be constant functions?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
because it is said in the book that four ODEs are needed to enclose the ODEs on C(t) and D(t),
then I just did this according to the instructions. what I posted above in my thread is just a part of optimization for ki (i=1,2,3,4).
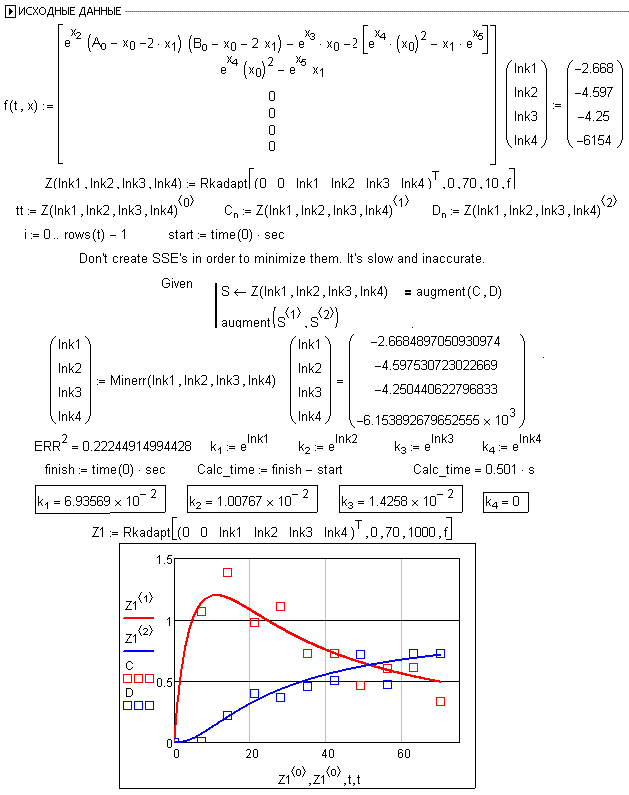
what I wanna do is to use ODEsolve block instead of RKadapt in the original file (as I attached below, Fig4.22 of the book I mentioned above, )
fig4.22
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So you can't expect a decent match with your datapoints because you never use them!
Whats wrong with the usage of Rkadapt? It returns (using 10 steps) exactly the 11 element vectors needed to compare with the datavector to fit which is done. If you use a solve block with odesolve you get a function and would have to construct these vectors yourself.
I don't think that you can find the values of your ki in an ODE solve block.
The construction in the original sheet makes sense: First define a function which solves the ODEs using the values of lki or ki as parameter. Then use this function in a Minerr block to find the optimal constants lki/ki. At last solve the ODE one last time using the just found constants but with more precision (more steps).
You can easily rewrite the last RkAdapt as an odesolve-block.
You could rewrite the first one, too, but it would be cumbersome to check against the original data points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think you have to do it just like it was done with Rkadapt. Odesolve can parameterize the solution without the parameters being one of the dependent variables. Rkadapt can only parameterize the initial conditions, so the parameters have to be passed as the initial values of dependent variables that do not change. Thus, your parameters can be independent of time in the Odesolve equations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes, u are right. I must compose the vector by myself, ODEsolve cannnot do it for me. thank you very much!
I had a very inflexible understanding for that example in the book, I will try to use the method mentioned in Fig 4.23
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
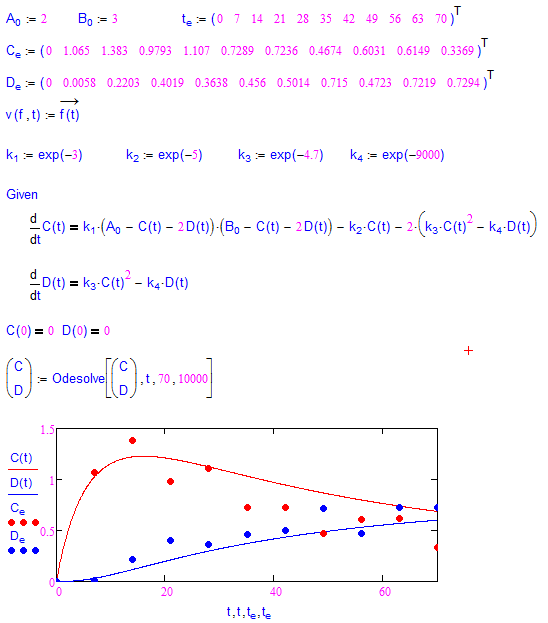
Is it something like this you are after?
I have changed your single scalars ki to a vector for compactness.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes, this is exactly what I want.
and I have recoded it in a similar way, but the calculation is much slower than that for the original example(maybe my calculations include too many steps), and my k4 is different from the old one.
your answer seems more close to what I want than that re-coded by myself![]() . I will study it, thx.
. I will study it, thx.
following is my codes (mathcad 14):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
and I have recoded it in a similar way, but the calculation is much slower than that for the original example(maybe my calculations include too many steps),
Yes, the 10000 steps slow down things considerably. Thats the reason for the additional steps parameter in my sheet.
your answer seems more close to what I want than that re-coded by myself
. I will study it,
Your code isn't that much different from mine. Differences are only that I changed the ki to a vector, used the vectorization directly without an extra function and used much less steps for ODEsolve in the Minerr block.
As for the different values - it seems that k4 (k3 in my sheet) has not much influence in the Minerr process as long as its smaller than about e^(-100).
I changed my sheet so the variables ki now ressemble the lnki of the original sheet, but still the same effect.
If you play around with the original sheet you will see, that its quite sensible witch respect to the guess values, too.





