Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to set the condition for the solution of a 4th order equation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to set the condition for the solution of a 4th order equation?
Hi All, I have a 4th order equation for an unknown parameter. The equation includes some constants whose number depends on the external setting.
The parameter must be a positive real number. In the attachment, I listed two possible symbolic solutions k2_1 and k2_2.
How can I set the if else condition correctly to achieve the following requirement?
(1) if both k2_1 and k2_2 are real and positive, show both of them as the solution of k2
(2) if only one of k2_1 and k2_2 is real and positive show this real number
(3) if neither k2_1 or k2_2 can satisfy the positive real condition, show an error message
Thank you!
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe something like the attached.
As you can see, as so often the symbolics ignores some constraints given via "assume".

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Introduce a new variable, e.g. 'x' with as definition:
x=k2^2, then your equations turns into:
(4/9)*x^2 - constant7*x + constant5 = 0
You can use simple school mathematics to solve x.
Then k2 values are found by taking the positive or negative square root of x.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are only 4 possible solutions (because it is a 4th order problem)
They are found with:

Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The other option is to ask Mathcad to solve the 4th order straight away:

Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe something like the attached.
As you can see, as so often the symbolics ignores some constraints given via "assume".

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner, I have a similar but more complicated calculation.
Now I have three variables with several constant numbers (depending on external setting). How can I get the symbolic solution of three equations?
My variables are k2, QE1 and QE2. Are are real numbers, and k2 must be positive. Would you teach me how to solve it symbolically?
It seems like I am not allowed to upload another worksheet in this thread. If you want me to open a new thread to upload the worksheet, I can do that.
Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You should not be limited in uploading worksheets. But the option to attach a worksheet is only available when you use the 'advanced editing' mode, or when you edit your entry (lower left corner: choose 'actions', the 'edit').
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you LucMeekes! I tried to solve the equations and Mathcad yields that the results are too large to display. Is there any way I can see the results individually? For example, can I see the symbolic results of k2, QE1 and QE2 separately? (the file is attached in this thread)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is an approach using a function with your eight constants as arguments.
As you can see Mathcad is not able to solve the sixth order equation it arrives at.
Not even with specific values for your constants, let alone with symbolic constants.

So you could try your luck using a numerical solve block. But you would have to provide a suitable guess and also you would get just one solution for each variable. To get another solution you would have change your guess.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As Luc already explained you sure are allowed to add more worksheets but this system makes it unnecessarily difficult to do so.
As an alternative to manually switching to the advanced editor you could send your message at first without attaching your file. Then, when you chose "Actions" at the lower left and then "Edit" you will end up automatically(?) in advance mode.
To solve a system of 3 equations in 3 variables symbolically you either pot the equations in a 3 x 1 vector and the use the symbolic "solve, var1, var2, var3" or you setup a solve block (Given ..... Find) and evaluate this block (the finat "find") symbolically.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner, thank you! Would you advise my question in the thread right above your reply?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just was about to edit my previous post as I had just seen you already attached your file and used the vector method anyway.
It looks like the result of your symbolic eval is not a normal 1 x 3 matrix as whenever I try to assign it a variable I get the message "variable not defined" !?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Werner! I have some update in my calculation. If we take a step back and we do not need to worry about my previously mentioned 3 unknown variable stuff, would you teach me how to solve this fourth order symbolic equation in mathcad? It seems like a direct solve cannot work in Mathcad. Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's no problem to solve that equation with Mathcad (11). Here's an extremely small part of the result:
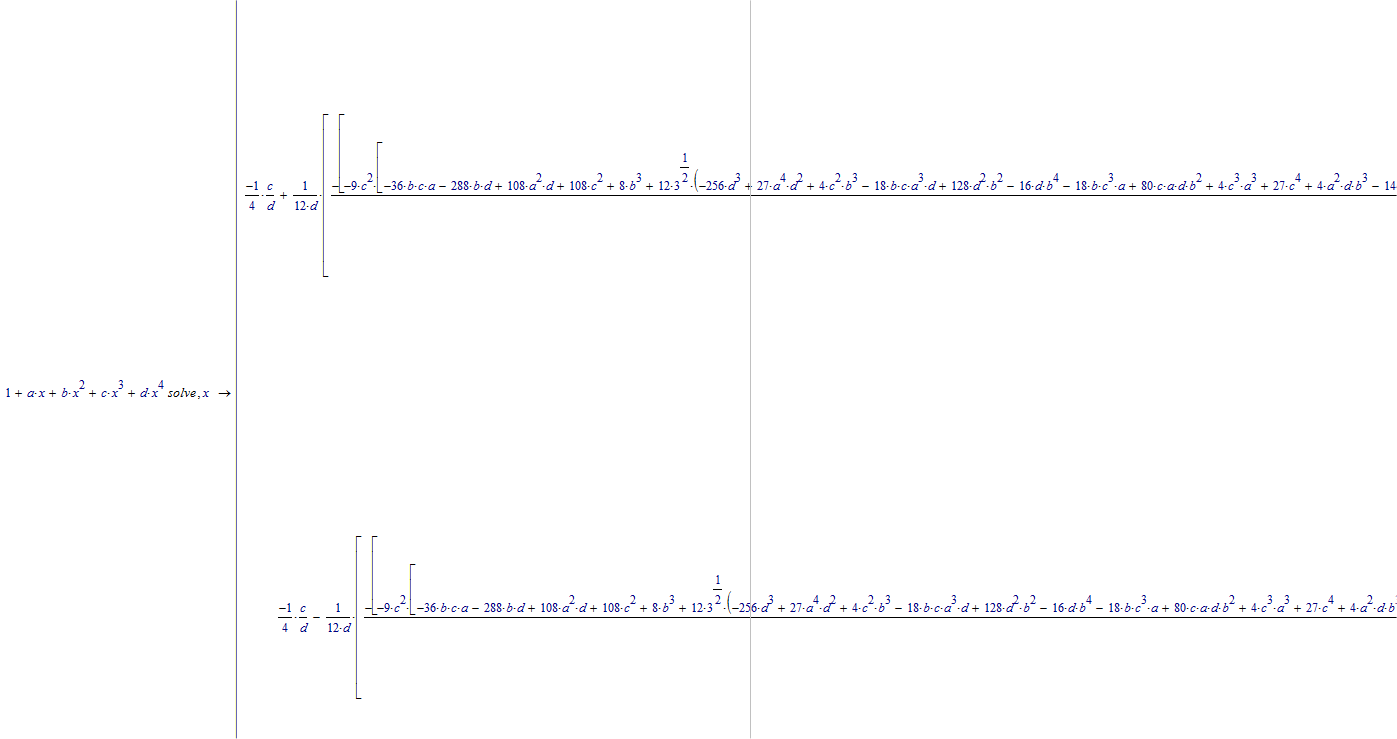
For further information see here Cubic equation with complex coefficients. this is on a 3rd order polynomial, your 4th order gives much bigger results!
This is as far as I can zoom out (10 %), every vertical bar marks a page; and you're looking at the first fraction only, but it is clear that there are 4 solutions:

Even mathcad 15 should be able to do it but likely will not show you the answer, and instead tell you that you can use the answer in further calculations.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> It's no problem to solve that equation with Mathcad (11).
It is in Mathcad 15 (and other version using MuPad as symbolic processor) as you can see in my reply ![]()
> Even mathcad 15 should be able to do it but likely will not show you the answer, and instead tell you that you can use the answer in further calculations.
True, but this can be quite tricky as my reply shows.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And of course, matters are much simplified if you can give the values of your constants up front.
Example:

Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The symbolics in Mathcad (= an old subset of muPad) can be quite cumbersome and sure is far below the capabilities of Mathematica or Maple (Maple is the symbolic engine in Mathcad 11 and so Luc is able to outperform us 😉
Here are some remarks:



- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner, thank you so much for this detailed calculation. One problem I got in editing your worksheet is the function "trim". My mathcad 14 cannot recognize this function. How can I use the equivalent function to replace "trim"? Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"trim" is a routine from the "Data analysis extension pack". Thats one of four add-on packs which usually were included with Mathcad. As far as I remember they were not included with educational single user student licences.
trim simply removes all entries/rows) in the first argument vector(matrix) at the positions given by the second argument vector.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's a trim alternative
Its a quick hack - no error checking, etc.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Werner. I am using a corporation license instead of the educational student license. It is strange that I do not have it. Do you have any suggestions to use the alternative method to achieve the same thing? For example, can we use "if" and "otherwise" to do this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just posted a workaround / trim replacement one minute before your reply 😉
I am not sure but maybe you had to pay for those extension packs at the times of MC14. I am pretty sure that they were free addons which came along and got installed automatically with MC15 using a regular license (singe user or corporate float). But I saw a student license of MC15 though were the help files/e-books got installed but the license would lock the features.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Of course you don't need to duplicate "trim" or use a replacement.
The filtering could be done in many different ways - here's one of them:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Werner, that helps a lot!
I have an additional question. If for this 4th order equation, if we know there will be 2 real solutions and 2 conjugated complex solutions, is it easier to get the symbolic solutions of them? Or there is no difference from the general 4th order equation with all coefficients unknown?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess that this knowledge does not help to find the symbolic solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 11 will solve this system purely symbolically, but the result contains root functions:
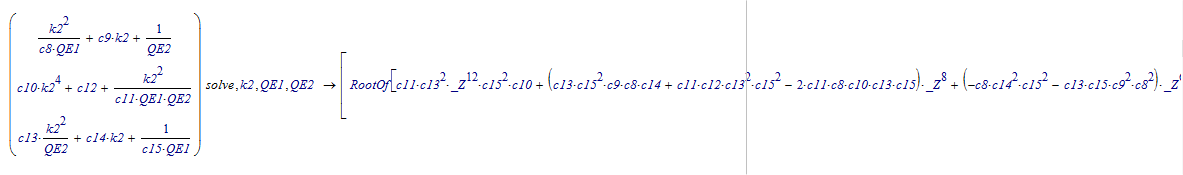
This is the full solution:

When provided with actual values for the eight constants you might get:

In this case, only the first (top) two sets of answers satisfy your requirements (QEi are real and k2 is positive)
Success!
Luc





