How to set the condition for two variables in solving symbolic equations

[yhuang-3]

Hi All, I have a two equations to solve and want to get the symbolic expressions of two variables. One of my variable k1 is a real number and assumed to be much larger than 1. Another variable Q6 can be either real number or have imaginary component.

If no condition provided, it is a much higher order equations for k1 and Mathcad returned no solution. How can I set the conditions to "filter out" the unqualified solutions and get what I want? The worksheet is attached. Thank you!

[AlanStevens]

Mathcad does find a solution, it's just too big to display (even if you add 'assume k1 = real')!  If you assign the results to variables you can use those variables (but they are still too big to display).  The equations can be combined to produce a cubic in k1^2, but even with this Mathcad says the solution is too big to display.

However, why do you want to see the symbolic result?  Try assigning numbers to all your constants and see if it produces a numerical solution (you could assign the result to a function, whose arguments are the various constants, should you wish to find the results for different sets of constants).

Alan

[yhuang-3]

Hi Alan, thank you for your response. The reason to use the symbolic solution, instead of using the real numbers in the expression, is to provide the users the freedom in calculating the target value in their applications. They can simply enter the numbers they want for each variable, and the worksheet can tell them the results according to the symbolic solution.

[AlanStevens]

yhuang-3 wrote:

Hi Alan, thank you for your response. The reason to use the symbolic solution, instead of using the real numbers in the expression, is to provide the users the freedom in calculating the target value in their applications. They can simply enter the numbers they want for each variable, and the worksheet can tell them the results according to the symbolic solution.

That's exactly what the numerical solution does when you make it a function - you plug in the numbers you want for each variable into the function arguments - you don't need the explicit symbolic solution.

For example (obviously I've just made up arbitrary values for the constants here):

Alan

[RichardJ]

If I assume K1 is greater than 1 (or even that it's real) Mathcad can't find a symbolic solution. You can look at your solutions with a little trickery. Sort of, anyway.

[yhuang-3]

Hi Richard, your solution is very helpful! I have two questions about your solution:

(1) I am trying to plug in some practical numbers into WW,XX,ZZ to further simplify them, and would you tell me if I can input more specific range for  WW,XX,ZZ? For example, if in practical, ZZ is between 0.25 to 8, can I define this in Mathcad?

(2) what is the meaning of the expressions like signum(WW,0)^5 in the solution?

[RichardJ]

(1) I am trying to plug in some practical numbers into WW,XX,ZZ to further simplify them, and would you tell me if I can input more specific range for  WW,XX,ZZ? For example, if in practical, ZZ is between 0.25 to 8, can I define this in Mathcad?

Yes, use the RealRange keyword. It's unlikely to help in this case though.

(2) what is the meaning of the expressions like signum(WW,0)^5 in the solution?

Signum (WW,0) returns 0 if WW is 0 and WW/|WW| (which for real WW is the sign of WW) otherwise.

[LucMeekes]

The essential problem is the fact that to solve this, a 6th order equation must be solved.

See the rootof() functions where _Z must be solved.

That's above the capabilities of symbolic solvers as far as I know.

Success,

Luc

[yhuang-3]

Hi LucMeeks, do you think there is any solution to simplify this 6th order equations? As I understand, if k1 is a real number and Q6 can be either real or have imaginary component, it does not help in simplifying the expressions? If so, can Mathcad help/we do it by ourselves in ignoring some terms to simplify the solution? For example, if I assume k1>>1, that means k1^2>>k1^(-2), so some of the terms can be ignore.

[RichardJ]

if I assume k1>>1, that means k1^2>>k1^(-2), so some of the terms can be ignore.

Yes, but it does not mean A*k1^2>>B*k1^-2, unless you also make assumptions about the relative magnitudes of A and B.

[AlvaroDíaz]

Hi. You must to get more accurate information. Q5 (or Q6?) can't be complex if all others are reals, just because the first equation. Regarding second, if Q6 have some imaginary part, between all others reals, must to came from some negative sign under the root, and cancel with the imaginary part of Q6, because the lhr therm is real. The information about k>>1 usually is implemented before the "main" calculus, through some convenient transformation for "prepare" some convenient approximation under the calculus. Usually, also, to do this pretty sure you must to know the sign for the quotients in the equations (this is, maybe not if Vo or Vin, H0 ... H4  are pos or neg each one, but know if have same or opposite signs, etc.) Are you sure that k1 can't complex, and what is more greater than one is abs(k1)? Can you tell us what is the meaning of the quantities in the equation?

Regards.

[yhuang-3]

Hi Alvaro, thank you for your reply! Actually this two variable equations are derived from another discussion, where you provided very useful input. (Would someone help me in finding out how to solve an equation) . A lot of help was obtained from you, LucMeekes and Hero of the Month: Richard Jackson in deriving this.

Your feedback reminds me that my derivation may have some questionable steps. Attached is the detailed derivation from the original problems in  Would someone help me in finding out how to solve an equation

to the equations shown in the thread, with a typical case numbers.  Would you take a lot and advise me how to solve it?

Thank you!

[LucMeekes]

Ok, there's more to say:

If you elaborate, you can get an expression for Q, where Q appears up to Q^6, but fortunately only in the powers Q^6, Q^4 and Q^2. This means that Z=Q^2 gives a third order expression, which IS symbolically solvable.

Here goes:

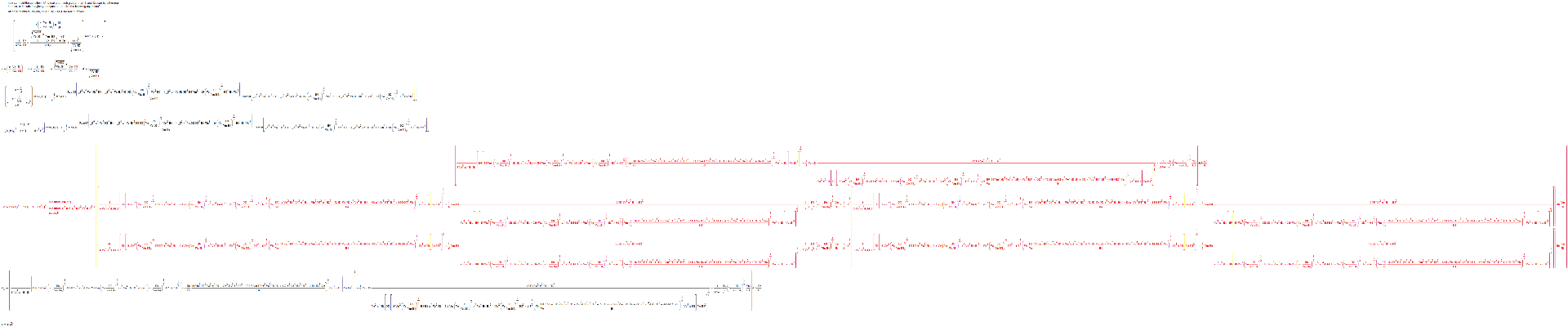
From the result you can determine Q6 and k1.

[LucMeekes]

That (above) is hardly readable,

Here is the stuff without the solutions:

Success!

Luc

[RichardJ]

It can find a solution. Six of them in fact (at least, the Mupad engine can, I haven't tried the Maple engine). It just can't display them because they are huge.