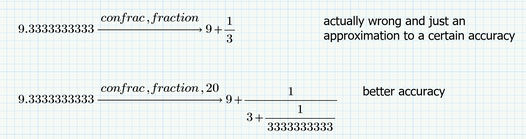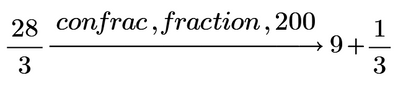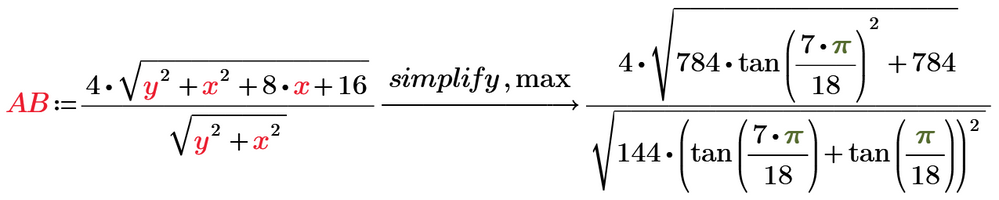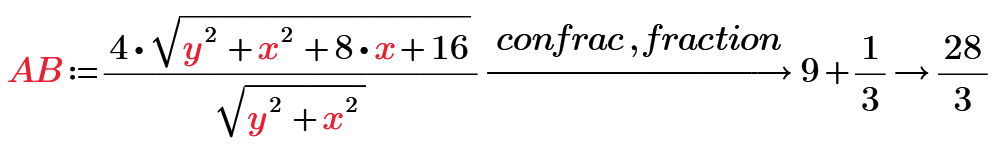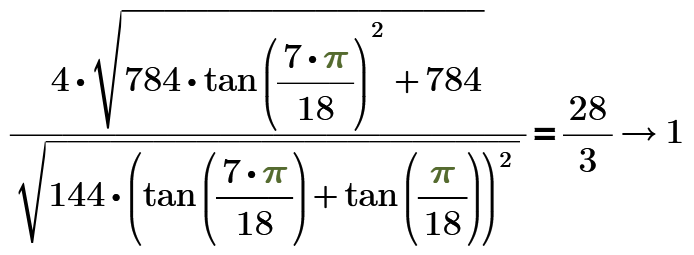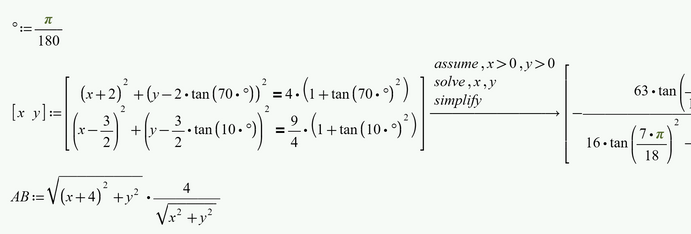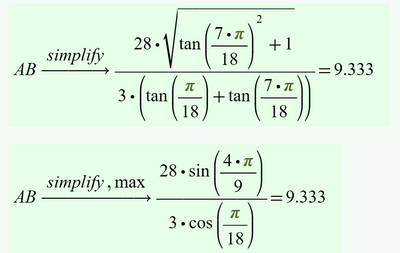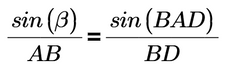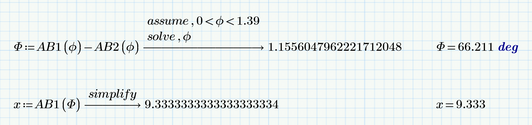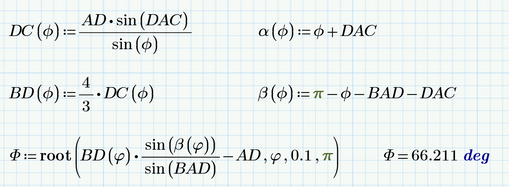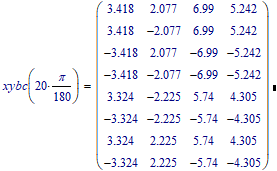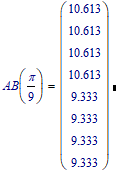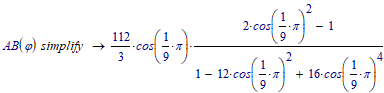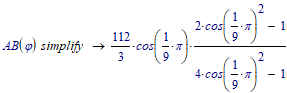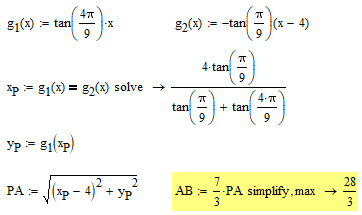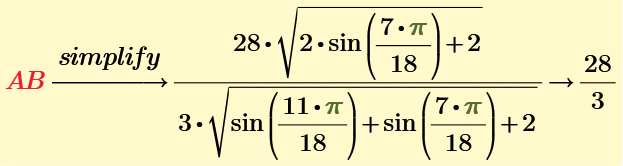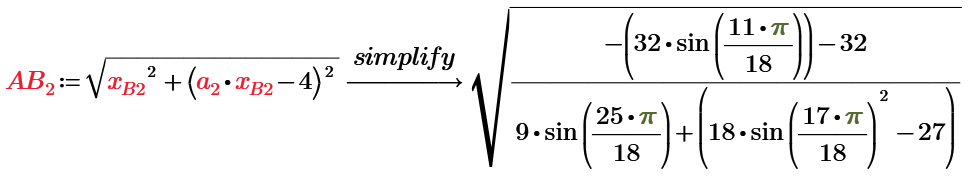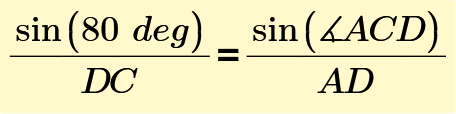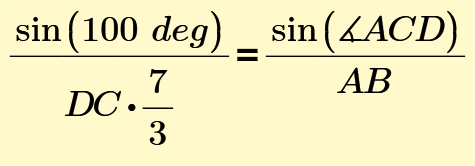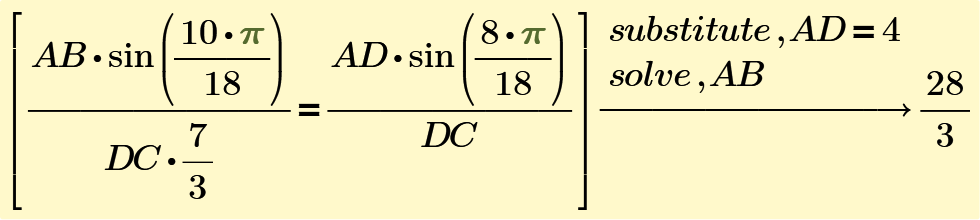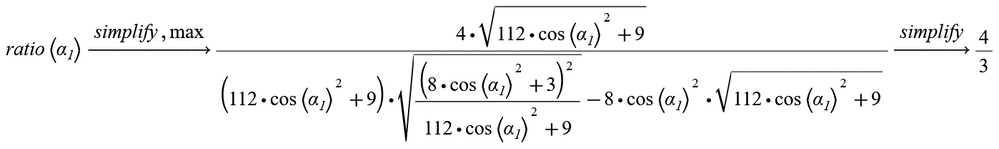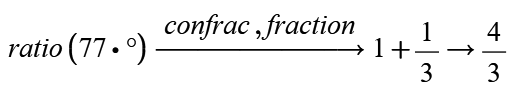- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
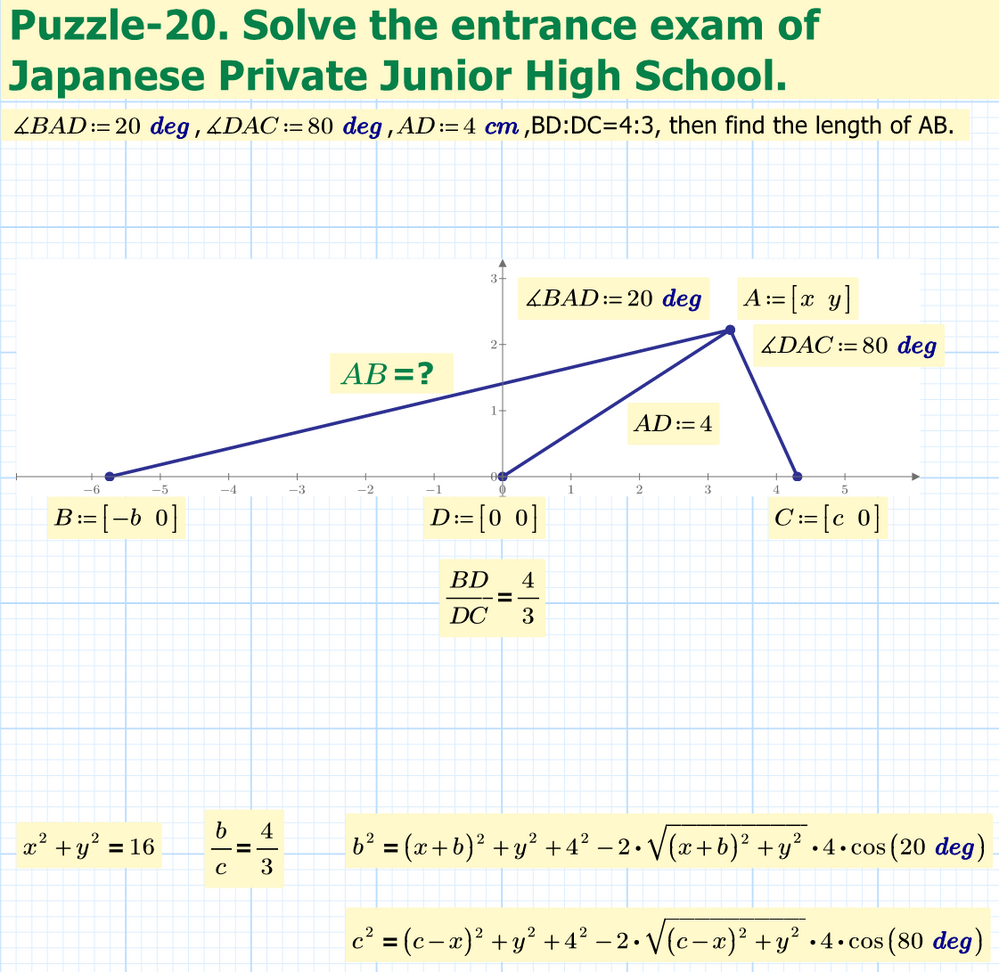
How to solve an entrance exam of Japanese Private Junior High School.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to solve an entrance exam of Japanese Private Junior High School.
- Labels:
-
Algebra_Geometry
-
Puzzles Games
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you all try to this puzzle. Now, we can solve another one by Mathcad Prime 8.
Find BD:DC=?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have already set up four equations with four unknowns. So you could use a numeric solve block (add constraints like x>0, y>0, b>0, c>0) or the symbolic solve.
Maybe you did in the sheet but I can't open it with P6 using the usual trick of exchanging the app.xml - maybe you used some new features not available in P6.
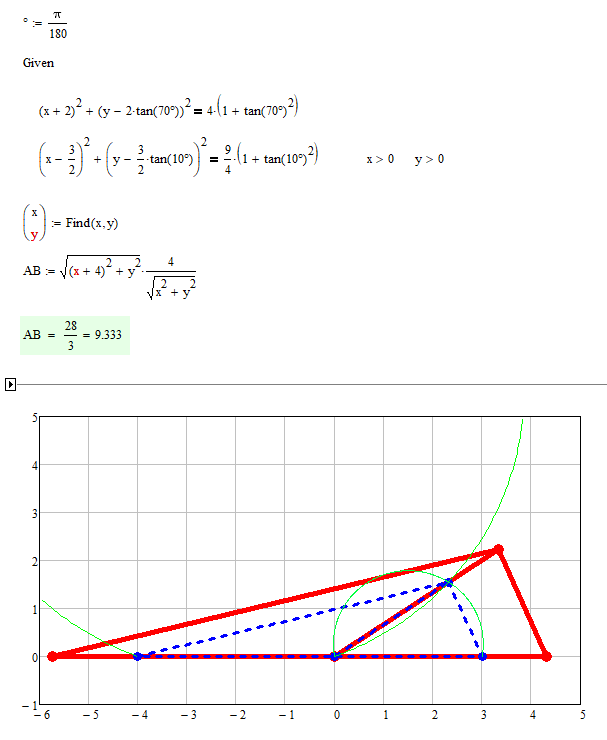
Here is a different approach (of course done in real Mathcad 🙂 )
Worksheet attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks.
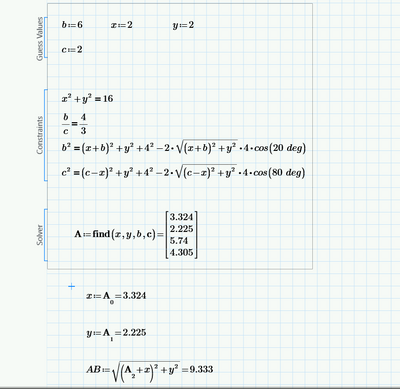
So I see he did not attempt a solution but just provided the four equation. In his collapsed area he used the solution 28/3 to calculate the points for the plot.
Prime cannot solve his system symbolically. Both engines throw a "no solution found".
I haven't tried but a numeric solve block should do the job but we won't be able to arrive at the exact solution 28/3 that way.
My approach simply followed the idea "how would I draw that figure with pencil, ruler and compass".
But being an entrance exam for Junior High I suppose there must be a much easier approach to solve the task.
Looks like this private school is going for the bests ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is indeed a very challenging problem for a school entrance exam. Here's my two cents: the actual test is multiple choice and several answers are provided. Then, it's a reasonably straightforward geometry task (law of cosines, law of sines) to try them and see which answer actually works with the constraints. No derivation required. but still rather time consuming. So it's testing iteration ability, not derivation ability. But that's only my guess.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yeah, as I suspected a numeric solve block does the job. I was too lazy to try as it was clear that unfortunately this would not give us the exact solution 28/3.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice!
But while we know that this fraction really is the correct exact solution, we can't be sure about it if we only use a solve block which relies on numerical (approximation) algorithms. The solve block yield 9.3333333... up to the IEEE precision of about 14-17 decimals and the symbolic confrac,fraction actually delivers a wrong result (because the input value consist of only a finite number of 3's).
Actually what we see is this:
An exact result would be
So the point is that it could be possible that the true exact result is so close to 28/3 that the symbolic "confrac,fraction" with standard precision returns 9+1/3 but actually the true result could be slightly off. It actually isn't but as soon as we use just one numeric only algorithm in the chain of calculations we cannot know for sure.
I still wonder about a much simpler approach to solve this task as I guess the candidates for that private junior high would not be allowed to use any CAS or other high tech tools to master the exam.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is the answer for 12 years children. Prime 8 only solve this puzzle numerically even using Werner_E's method.
This shows only both side of = sign is almost same.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
This is the answer for 12 years children. Prime 8 only solve this puzzle numerically even using Werner_E's method.
My solution is a pure symbolic one and so far exact and not a numerical approximation! I think it should be possible to do it in Prime, too. As Prime does not allow to symbolically evaluate solve blocks, you would have to use the symbolic "solve" with the modifier "assume" for the constraints (x>0,y>0). I am not sure it the new symbolic engine is capable enough, though.
BTW, it was just in the last step that I had to help Mathcads symbolic a little bit to get rid of sine and cosine to arrive at the simple solution:
The calculation in your posting uses already defined x and y and you don't show how you defined them. If you did it as in the sheet you posted, you already used the solution 28/3 to finally show that the solution is 28/3. That would be a kind of circular reasoning, no proof at all. 🙂
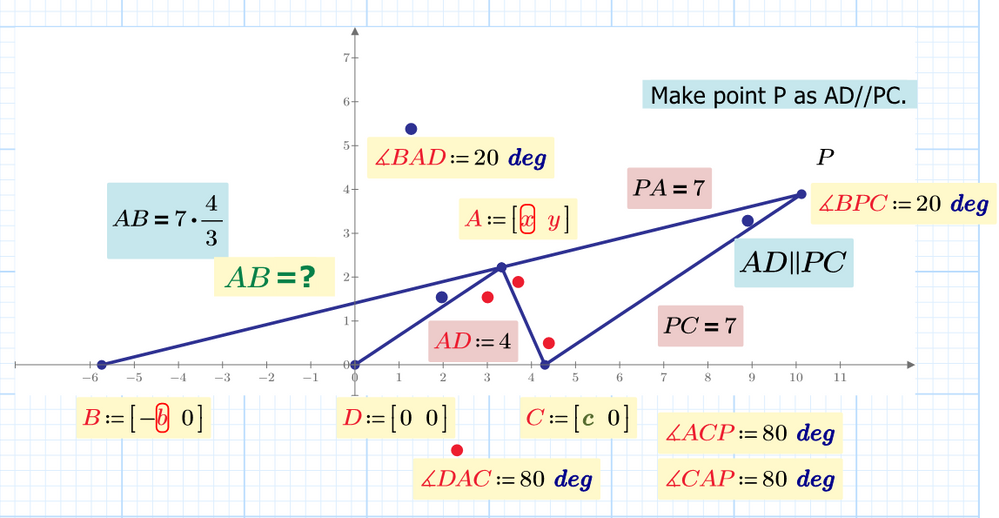
The explanation for the 12years old which we can deduct from you sketch is very nice but also quite tricky! The angles are only used for 20°+80°+80°=180° and if you see this and the various ratios 4:3 or 7:4 involved, you could tell the solution AB=AP*4/3 = 28/3 out of your head without any manual calculations and without using trigonometric functions - just using the intercept theorem and/or the ratios in similar triangles.
Really clever, but how many 12year olds would come up with this solution? I guess I know of none who would be able to ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
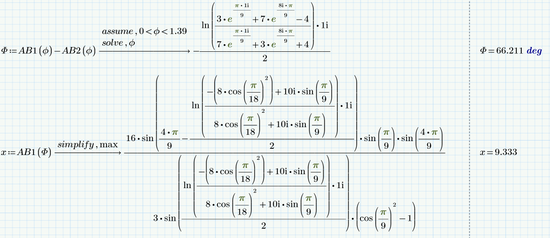
OK, I gave my approach a try in Prime.
Symbolic solving worked OK
But when it came to simplifying the expression for AB, the new symbolic once again failed.
Here the results with the old symbolic engine (muPad):
As already written above, in the last expression its necessary to tell muPad that the sine and cosine are equal because the angles add up to pi/2.
Here what the new symbolic does (after a very long time of "thinking"):
The modifier "max" uses up all memory and then fails without returning any result 😞
I can't check but the "result" may be the same in Prime 8 as well. Don't think the symbolic engine really has significantly improved.
So once again it proves that in current versions of Prime its better to avoid symbolic calculations - they seem to are not worth the effort and hassle to find suitable workarounds.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I thought this was going to be simple!
I appear to be missing a constraint. Prime 4 Express attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
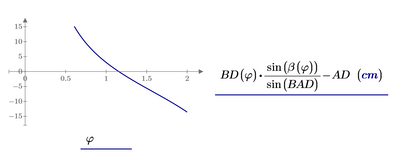
An error lies here
Either write AD instead of AB or exchange sin(alpha) for sin(beta).
One additional constraint you are looking for could be a second way to calculate AB
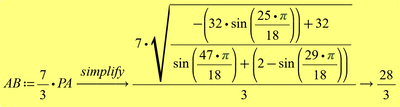
BTW, the value for AB is not 9.333 but exactly 28/3 which of course can't be proofed by using numerical algorithms like "root".
But symbolic calculations fails, too, to proof the result is 28/3.
The new symbolic switches to float mode and so the result is unusable for a proof:
The old symbolic succeeds in an exact solution for phi but fails to simplify AB down to be 28/3:
I really like the solution sketched by ttokoro using just some ratios and avoiding trigonometry completely, but I still wonder which 12 year old would be able to come up with that kind of solution to pass the entrance test. I guess I myself would have failed ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here another suggestion for an additional constraint to get the value of phi. We calculate the length of AD using BD, beta and BAD and check, if its equal to predefined value AD=4
Here the choice of the range for phi is less critical so we get a good result even by using the large range from 0.1 to pi
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks to Werner I was shown my error.
And after too many false starts---the answer! A different file of the same name attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice solution, too.
I tried to solve symbolically (to get the exact 28/3) but to no avail as the symbolic engines (both) will switch to float mode when solving for Phi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 11 finds 2 different solutions:
One symbolic solution is:
another is:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
Mathcad 11 finds 2 different solutions:
The "solution" where AB=10.6 isn't a solution to the original problem because here the angle DAC is 100 degree and not 80 degree as demanded.
The last equation in your set of four isn't fulfilled with that "solution".
Looks like Maple squared the last two equation when it solved the system and "forgot" to discard the invalid "solutions" we may get when we square an equation.
I wonder if Maple in MC11 would be capable enough to come up with the exact solution 28/3 - either with ttkoros initial setup or the way Fred approached the problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
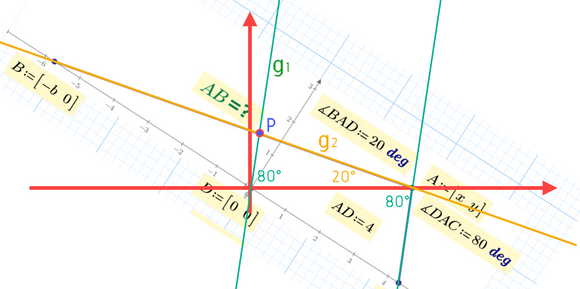
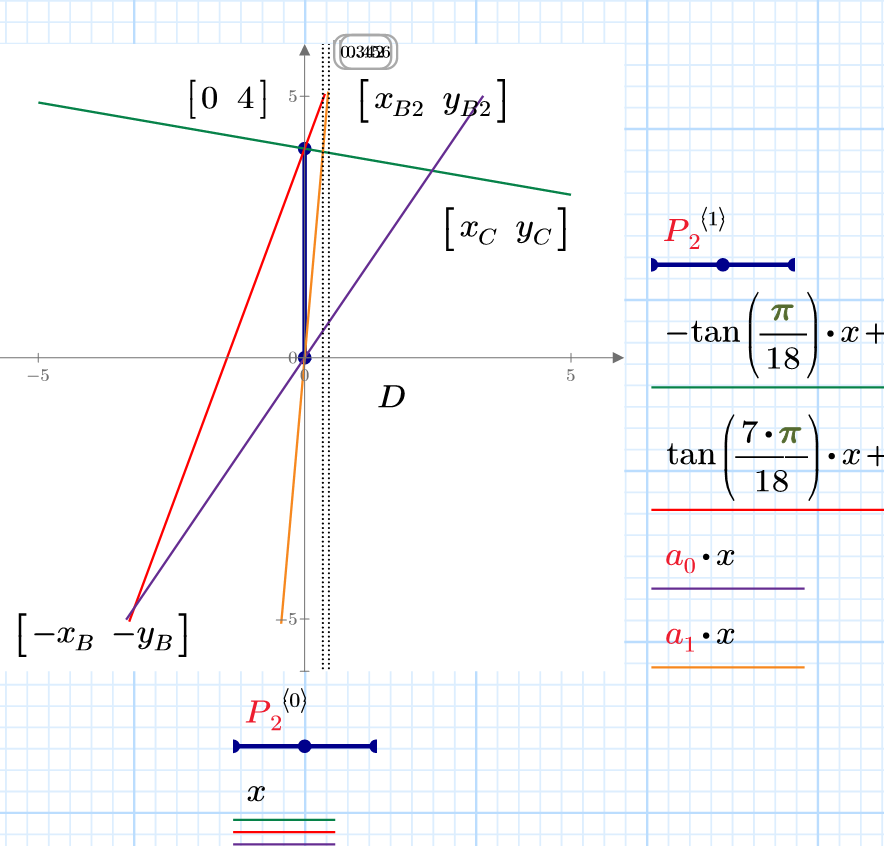
OK, I thought of a second way to draw the figure using pencil and ruler and now the calculation is much simpler.
I use a different coordinate system with D(0/0) and A(4/0).
The parallel g1 to AB through D and the line AB intersect in P and because of BP:PA=PD:DA=4:3 we have AB=7/3*PA.
So the whole calculation simplifies to
I haven't tried but I guess that even Primes new symbolic engine should now be able to arrive at the exact solution.
Remark: Of course in the picture we see at a glance that in the triangle DAP the angle at P is 80° as well (all three angles must add up to 180°) and so we have an isosceles triangle with PA=DA=4. So we can tell without further calculation that BA=7/3*PA=7/3*4=28/3.
This is similar to what @ttokoro already had shown as the solution for (or from) the 12 year olds 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
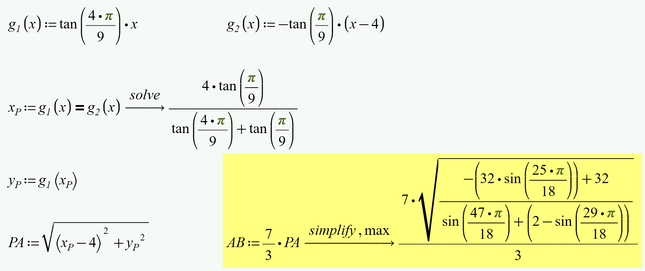
I haven't tried but I guess that even Primes new symbolic engine should now be able to arrive at the exact solution.
OK, now I gave it a try and it seems that I was wrong. The new symbolic engine can not even simplify this expression - at least not in Prime 6 (the legacy engine of course succeeds).
The new engine is now calculating for quite some minutes and I don't have the patience to wait for this calculation to perhaps end at some point. Possibly again without result and with the "out of memory" error message ...
I attach the Prime sheet if anybody likes to give it a try himself.
EDIT: Of course I was curious and let Prime work in the background. Here's the result: 😞
Without the modifier "max" we get the very same result, but much faster.
EDIT 2
Incredible! A second symbolic evaluation does the job! Why, oh why, doesn't the engine get it right on the first run???
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime 8.
Not the answer but same lines.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using the law of sines in the triangles,
Therefore,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you all try to this puzzle. Now, we can solve another one by Mathcad Prime 8.
Find BD:DC=?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
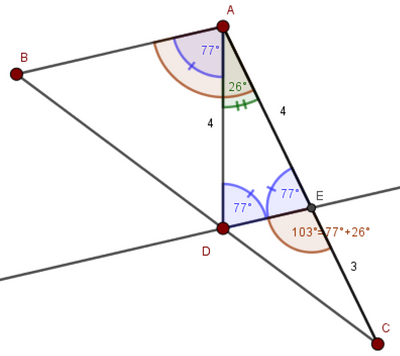
4:3 w/o calculation.
Actually thats nothing significantly new compared with #20 because 2*77°+26°=180° similar to 2*80°+20°=180° in #20.
So AB // DE ...
Looking forward for an exact, symbolic solution in Mathcad or Prime 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The symbolic engine seems not to be capable enough.
Of course the result is always 4:3 independent of the input value alpha.1
The symbolics only succeed for 75° / 30° instead of 77° / 26°
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime 8
The last 3 equations only can that and can't simplify, max.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah, thats fine! At least the first one with generic angle. Even though its sad that it needs that second "simplify" and can't do it in one go.
The other two are not exact symbolic solutions because "confac,fraction", while being a symbolic modifier, is just sort of a numeric method as shown earlier in another answer.