Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to symbolically derive a function with respect to a function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to symbolically derive a function with respect to a function
Please see the attachment.
In Lagrange Equation for Dynamic equation,
there is a term that request the derivative of T(t) with respect to (u(t))',
I don't know how to achieve this.
Looking forward to your help!
Thank you very much!
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From what I see you have this (assuming your formulation is correct):
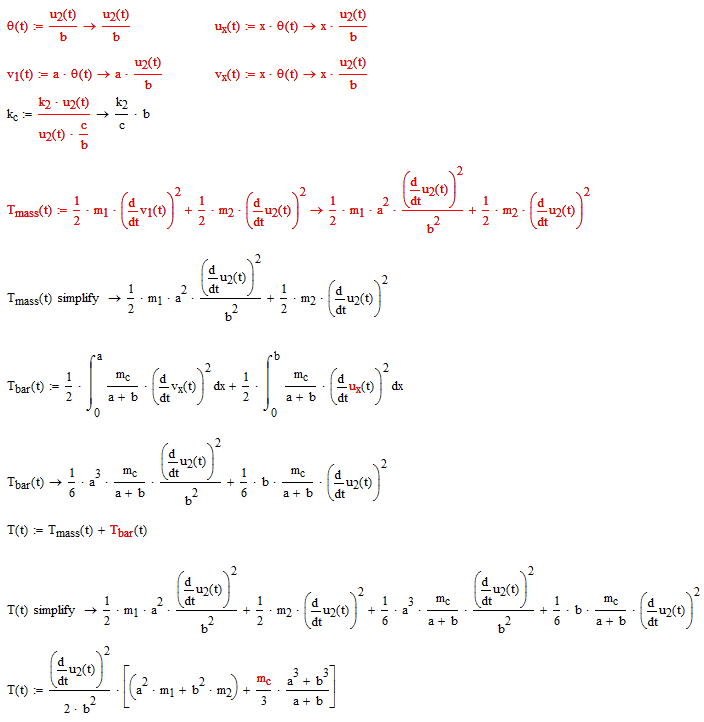
Which means you have a function T(t) which is found from the function u2(t) by first taking the derivative of u2(t) with respect to time: u'(t)=d/dt of u(t). Then square the resulting function squ'(t)=u'(t)*u'(t). Then multiply the result with a constant (assuming that a, b, and the three m's are known). This should be simple, provided that u2(t) is given...
Are you sure you don't need a second derivative of any functions u and v, rather that the first derivative squared...?
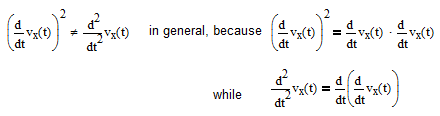
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From what I see you have this (assuming your formulation is correct):
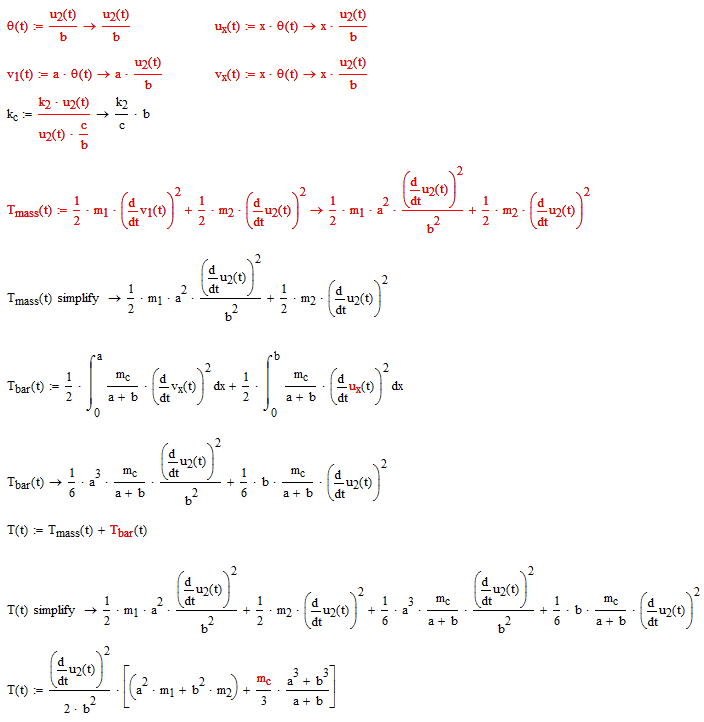
Which means you have a function T(t) which is found from the function u2(t) by first taking the derivative of u2(t) with respect to time: u'(t)=d/dt of u(t). Then square the resulting function squ'(t)=u'(t)*u'(t). Then multiply the result with a constant (assuming that a, b, and the three m's are known). This should be simple, provided that u2(t) is given...
Are you sure you don't need a second derivative of any functions u and v, rather that the first derivative squared...?
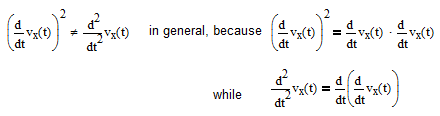
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi, Luc
So by this step,
Is it possible to let Mathcad derive T(t) with respect to du2(t)/dt?
Which will result in:
It is to set du2(t)/dt as the argument and the others (including u2(t), if exists) as constants.
Thank you
Best
Shawn
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Shawn,
No, If you feed that first expression AND u2(t) to Mathcad it will take the deriverative of u2(t), then square it and multiply the resulting function with the constant involving a, b and the three m's. The result you mention is NOT obtained.
Observe my question/comment at the end of my first reply:
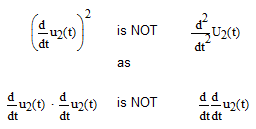
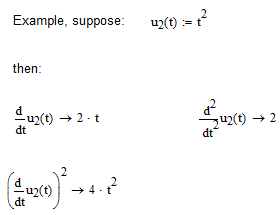
Success!
Luc





