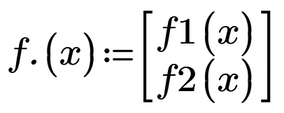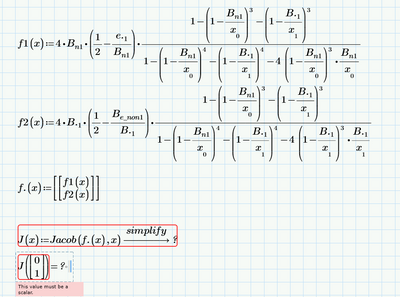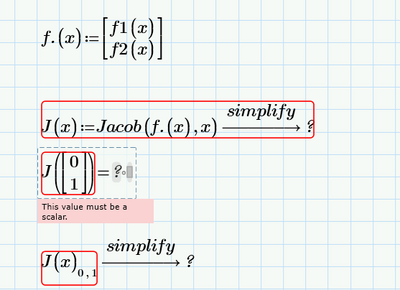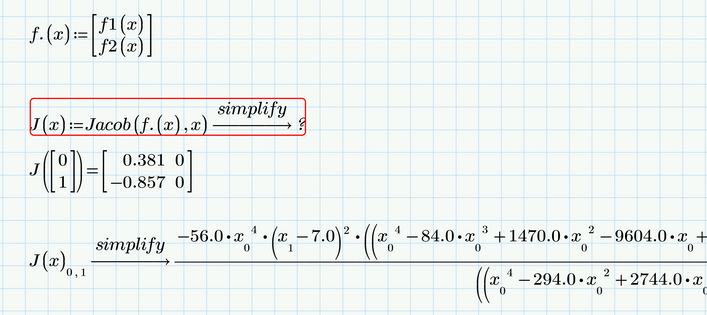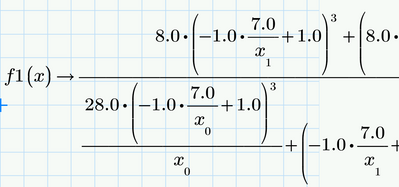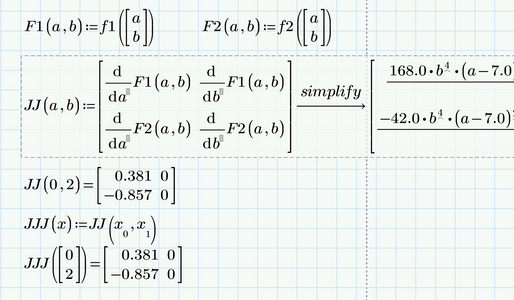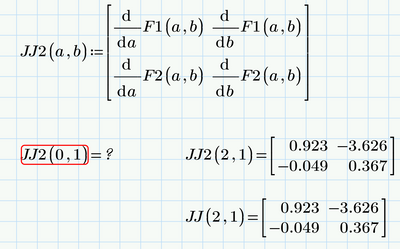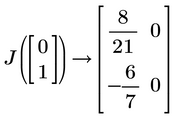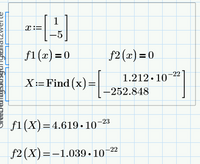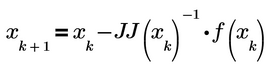Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
I'm having difficulty setting up a multivarate newton-raphson function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm having difficulty setting up a multivarate newton-raphson function
I'm having a hard time setting up the function to solve. Any help would be appreciated. I've attached a file of what I'm working on. I'm using MathCAD Prime 8.
- Labels:
-
Calculus_Derivatives
-
Mathcad Usage
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- By default vector- and matrix-indices start with 0, but you used index 1 and 2 in your definitions.
You can do this, but you would have to set the system variable ORIGIN to 1. Either via the menu or simply type ORIGIN:=1 at the top of the sheet - Why did you define your function f.(x) as a nested matrix? A 2x1 matrix inside a 1x1 matrix. I guess a simple 2x1 matrix is all you need
- When you call the Jacob function you use f(x) as argument. But you called your function f.(x) (note the dot after "f", its part of the name
- You will get a message that the expression is to large to display but still van be used in further calculations. Thats an annoying "feature" but usually there is not much you can do. In your case you are allowed to display the four entries of the Jacobi matrix singly as shown in the picture below
BTW, as you already defined your functions f1(x) and f2(x), you should make use of them when you define f.(x)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for your help. I'm still having issues with setting everything up. What am I doing wrong at this point? Thanks, again for the help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the definition of f.(x) I still see two pairs of square brackets! That means that you still define a nested 1x1 matrix with a 2x1 matrix as its element.
You have to delete the outer pair of square brackets. It should just be a 2x1 matrix/vector with the two function definitions as its elements.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I updated the brackets and I'm still receiving the same error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Attach your file please.
As you are using P8 and I am using P9, it would not make sense posting my file as you would not be able to open it with your version of Prime.
BTW, is there a special reason you named the function "f." and not simply "f" ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's an old habit from MathCAD 15 where you could put a period to insert a subscript.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@JA_10710615 wrote:
That's an old habit from MathCAD 15 where you could put a period to insert a subscript.
I already thought that MC15 would be the reason or it.
I usually use variables like "t." when I need to define a range for plotting. It would look like a normal "t" but would not interfere with "t" as an undefined free variable.
I opened your sheet in Prime 9, let it recalculate without changing anything and it worked OK
I would have expected kind of a division by zero error if x[0 is set to zero ...
Maybe it worked OK due to a bug fix/improvement to the symbolic engine they made from P8 to p9 ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I vaguely remember of a bug in Primes symbolic engine which also turns matrix indices to float numbers, when the symbolic was forced to float mode (which is the case if non-integer numbers are used). Later calculations would then fail because of a vector index 0.1 or 1.0.
You can check if thats still the case in P8 by just evaluating f1(x) after you had defined the function. You should see
If you see x with index 0,0 and 1,0, then the bug still is present in P8 and was only fixed in P9.
Try to replace the 1.5 for variable e.1 by 3/2, let the sheet recalculate and see if it helps.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So it's an issue with the version of MathCAD I'm using. How would I setup the newton function to return answers?
I appreciate all of the help you've provided.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Did you try to replace the 1,5 by 3/2 as suggested above?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Of course you can always define the Jacobian yourself and see, if it works in your version.
Prime does not allow the derivation of a vector function, so we have to define "normal" auxiliary functions F1 and F2 with scalar arguments.
After calculating the Jacobian you may redefine it to take a vector as its argument instead of two scalars. You don't have to use different names as I did.
As you can see using this method we even get the symbolic answer displayed.
But I guess that it should not be necessary at all to evaluate the definition of JJ(a,b) symbolically if all we need are numeric results. Using the test vector you would get an error because of the division by 0 if a=0, but otherwise it works the same.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why did you choose the argument 2,1. Would I have to change the argument if I want evaluate different numbers? Is there a way to automate this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The evaluation of f1(x) returned the same solution you showed. I tried what you suggested for e1 and this is what was returned:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As far as I can see I did not use a symbolic evaluation but rather a numeric one.
But I just tried and I get
So all that can be said is that the implementation of the Jacob function seems to have been significantly improved in Prime 9.
You may try to upgrade if possible or use a user defined Jacobian function as shown in a previous answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
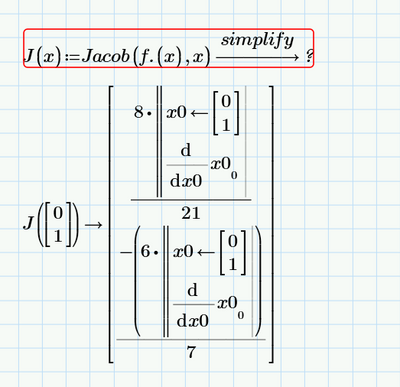
It's not displaying correctly, but it's working as intended.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may try to add the modifier "simplify" as I did and see if Prime would be willing to display the symbolic result or you may even use "simplify,max" (calculation takes longer, result sometimes, but not often, is simpler)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Where are the solutions to the original equations? It's not in the JJ Matrix correct?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Which solutions? Which original equation?
Do you say that the definition of JJ is not the correct one for the Jacobi matrix?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm trying to solve for x0 and x1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@JA_10710615 wrote:
I'm trying to solve for x0 and x1.
Solve which equations?
You never showed any equation(s) so far.
You just tried to calculate the Jacobi matrix of a vector function f. which is what JJ should do as Prime 8 fails using the built-in jacob function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Equations f1 and f2 are a series of two equations with two unknowns, x0 and x1. The jacobi matrix is part of setting up the Newton-Raphson method. This will approximate the values that satisfy the system of equations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Actually f1 and f2 are functions, not equations. Functions in one variable which is a 2-element vector.
So what should the equation be?
If it should be f1(x)=0 and f2(x)=0, then its a very unstable system where the solution found by Primes solve block are significantly dependent on the initial guesses.
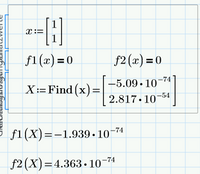
But anyway, whats wrong in your opinion with the way JJ calculates the Jacobi matrix?
You asked "Where are the solutions to the original equations? " Its you who has to know how to use the Jacobi matrix and apply it to Newton-Raphson to get an approximation for the solution of the system, aren't you?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nothing is wrong with the Jacobi Matrix. I don't know how to setup up the Newton-Raphson in MathCAD. That's what I was asking. The Jacobi matrix is part of setting up the Newton-Raphson and not the final step. I apologize if it came across as me questioning what you provided me thus far. The solve block only provides one solution while the Newton-Raphson will provide multiple solutions at a time. I already have an idea on what the output should be.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guess this new question may justify a new thread.
Basically you have to setup a loop which calculates a new vector x_(k+1) depending on the previous x_k, starting with the guess x_0 and using the iteration formula
The iteration may stop after a certain number of iteration steps or when a certain accuracy (distance of the current value of x to the previous one) is reached - better apply both conditions to avoid an endless loop.
Practical implementations avoid the calculation of the inverse of the Jacobi matrix and instead solve a system of equations via Gauß or similar.
See e.g. here
https://en.wikipedia.org/wiki/Newton%27s_method#Systems_of_equations
or with some examples here
https://www.math.usm.edu/lambers/mat419/lecture9.pdf
But again - your specific system is very unstable and an approximation method may give you "random" solutions depending on the guess vector.
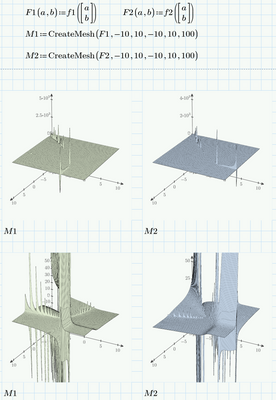
I have plotted the two functions and it looks like they return most of the times a value around zero with the exceptions of some "spikes". So there may be a lot of positions, where both are around zero (within numerical precision) and this could explain the many different "solutions" you get depending on the guess value. So its sure not the best example for learning and demonstrating the Newton algorithm - which seems to be the purpose, as otherwise you simply could use Primes built-in numerical method (solve block with "find") as shown in my previous answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm back to annoy you again. I read the lecture 9. I'm still confused as to how I set this up in MathCAD.