I'm having difficulty with this solve block problem

[Jay]

Any suggestions on how to approach this problem would be appreciated. Thanks.

[Werner_E · Accepted solution]

Here is one possible way to do it.

[Jay]

Werner,

As always, thanks for your prompt and detailed help. The solution you provided makes it obvious what I overlooked ... I needed that! Also, thanks for the "otherwise" usage help, it made it much more straightforward. Oh yes, thanks for leaving the clue to the definition case that I overlooked and left out as well.

Jay

[Werner_E]

You are welcome.

Looking at it again I still don't understand why the integral from 0 to infinity (we had that in another thread) does not work.

And in this example I don't understand why the first integral (from 0 to 0.1) works, because the integrand is not defined for the range from 0 to 10^-5). Mathcad - always good for a surprise 😉

[Jay]

Werner,

Yes, interesting.

There appears to be something there ... ?

However, this says otherwise ... ?

Perhaps there's some sort of round off residuals ... ?

It's over my head,

Jay

[Werner_E]

I am not sure what your second expression will show. You are aware of the fact that sqrt(a+b) is NOT equal to sqrt(a)+sqrt(b)!?

First we would had to agree upon what value(s) Ps should yield for 0<f<10^-5 and define the function accordingly.

I set the lower limit to 10^-5 instead.

Then some kind of scaling could do good - so it seems you are right about the round offs:

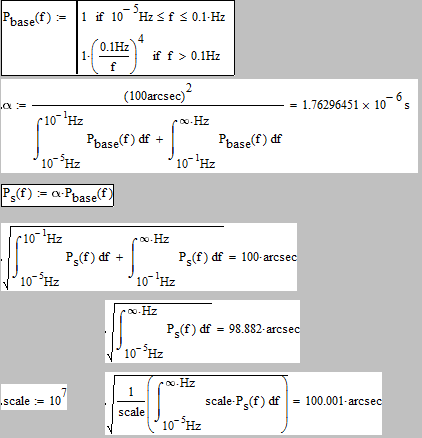
You see I catched on Alan's suggestion and omitted the solve block.

[Jay]

Werner,

Yes, thanks for keeping me on track! I apprciate your (and Alan's) time. Your scaling idea was very good, I wish I had thought of it. Your (and Alan's) insights have been very helpful. Thanks again.

Jay

[AlanStevens]

You might also notice that, in this case, it is a trivial matter to do the integrations analytically:

Alan

[Jay]

Alan,

Thanks for your input. Please share with me how you arrived at the 1/30 part ... it's not that obvious to me.

Jay

[AlanStevens]

As follows:

Alan

[Jay]

Alan,

Thanks for the explanaton ... I thought that you maybe had something in mind that didn't involve an integral. What you show is very clear. Thanks for your insight, this was helpful for my thought process.

Jay