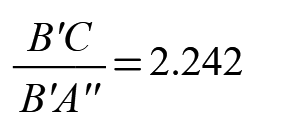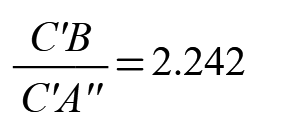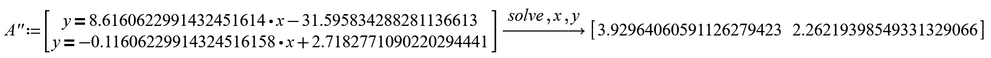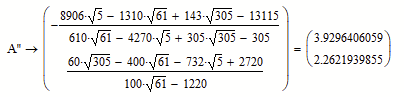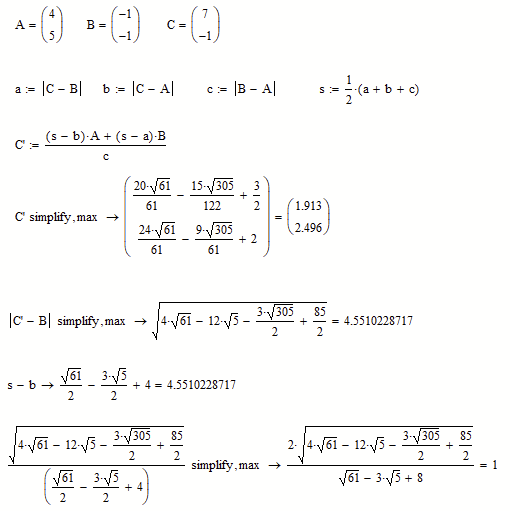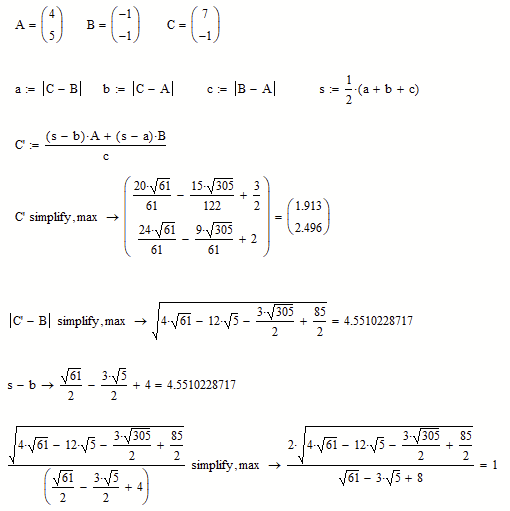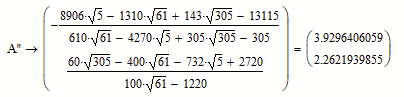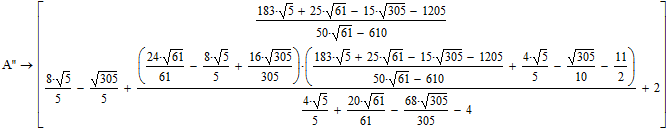Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Inscribed circle and altitude of triangle ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Inscribed circle and altitude of triangle ?
Hello Everyone.
Given :
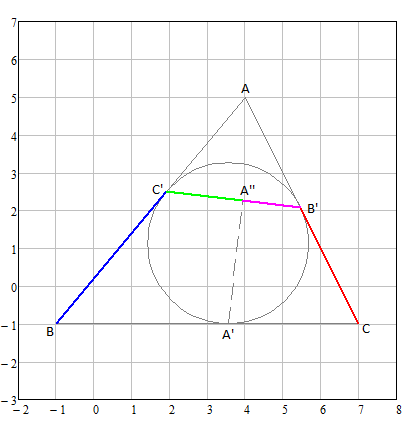
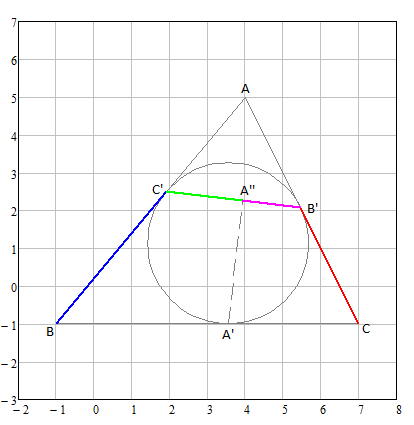
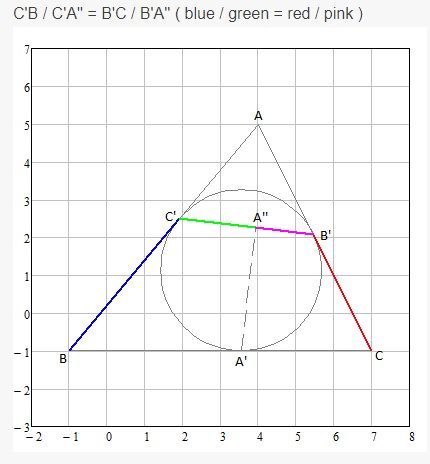
inscribed circle of triangle ABC touches its 3 sides at A', B', C'. (see Figure)
A'A'' is a altitude of triangle A'B'C'.
Prove :
C'B / C'A'' = B'C / B'A'' ( blue / green = red / pink )
Thanks in advance for your time and help.
Regards.
Loi.
- Labels:
-
Math Homework
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
Not equal.
No, you are wrong! The two ratios ARE equal. For the example posted approx. 2.24224.
Check your calculations or your interpretation of the position of A". Guess you misinterpreted the latter. A'A'' is perpendicular to B'C' ! The coordinates are approx. A'' (3.92964 / 2.26219).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Actually its
And the ratios are
Mathcads symbolic is too weak to proof that the ratios are equal - even if we provide specific numbers, let alone with symbolic coordinates.
- Tags:
- ctaually
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Werner, follow your hints : It seems Mathcads symbolic is power enough to proof that the ratios are equal.
I'm going to check out other case of the triangle.
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
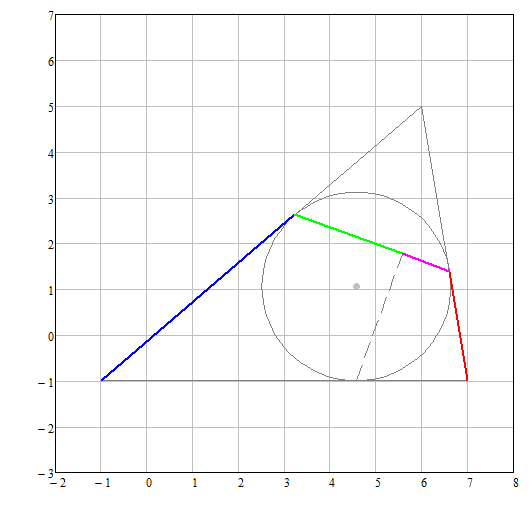
An other case of triangle :
It seems Mathcads symbolic is power enough to proof that the ratios are equal. (for 2nd-test)
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It depends on how the coordinates of the points are actually calculated. Obviously your way of doing it is more "symbolic-friendly".
You can see the weakness for instance if you compare the results of, lets say, the distance from B to C'.
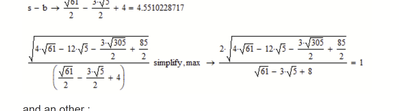
We can calculate it simply by s-b (where s is the half circumference) or "the hard way".
As you can see below, Mathcads symbolic is unable to proof that the two results are equal.
I may be that you found a different way to calculate the coordinates of C' and arrive at a symbolic representation which is better simplified.
A proof, however, would be to do the whole calculation with symbolic coordinates for A, B and C and I really doubt that Mathcads symbolic is able to do so, but I'm ready to be taught otherwise 😉
As you see, the symbolic is not able to simplify the expression to 1.
Of course Mathcad is also not able to proof with symbolic coordinates that the two methods for calculating the length of B-C' are equivalent:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
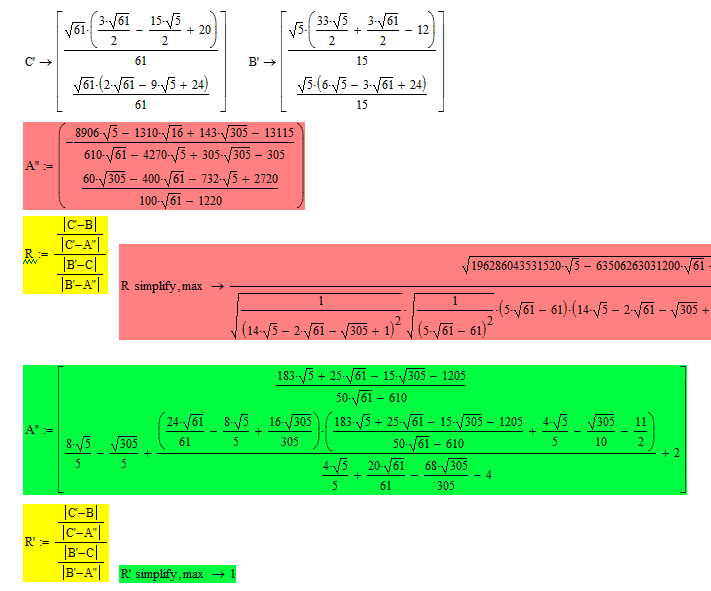
Werner, It seems Mathcads symbolic is powerful enough to prove that the above ratios equal 1.
and an other :
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@lvl107 wrote:
Werner, It seems Mathcads symbolic is powerful enough to prove that the above ratios equal 1.
I don't see that the symbolic result is 1! The 1 is the numeric result.
Furthermore we would need symbolic coordinates for a real proof 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"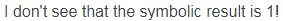
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I had not looked that closely and thought that the second half of your picture is an example with different values because you wrote "and an other :"
Its crazy that "factor" seems to do the trick and it does it only if the coordinates of C' are not simplified beforehand.
Did you try symbolic coordinates?
EDIT: I gave it a try and it failed even by adding just one symbolic coordinate
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner, without your *.xmcd file then the question is difficult to answer. (sometime cause misunderstanding). And I guess my answer is : " We should not symbolic coordinates of numerator and denominator, and only should symbolic the whole of ratio ".
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner, your calculation of coordinate of A'' is :
and an other calculation of coordinate of A'' is :
and the difference between two of the symbolic of the ratio is :
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, different representation give different (but equivalent) symbolic results. I notice that less simplified input expression sometimes seem to help to give a better simplified symbolic end result. But in all thats quite unsatisfactory and unstable.
I guess that its not possible to really prove the assumption with Mathcad as this would mean to work symbolically without specific values for the coordinates. But at least it seems that you found a way using your method of calculating those points, to prove it for specific values. Thats at least a partial success 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
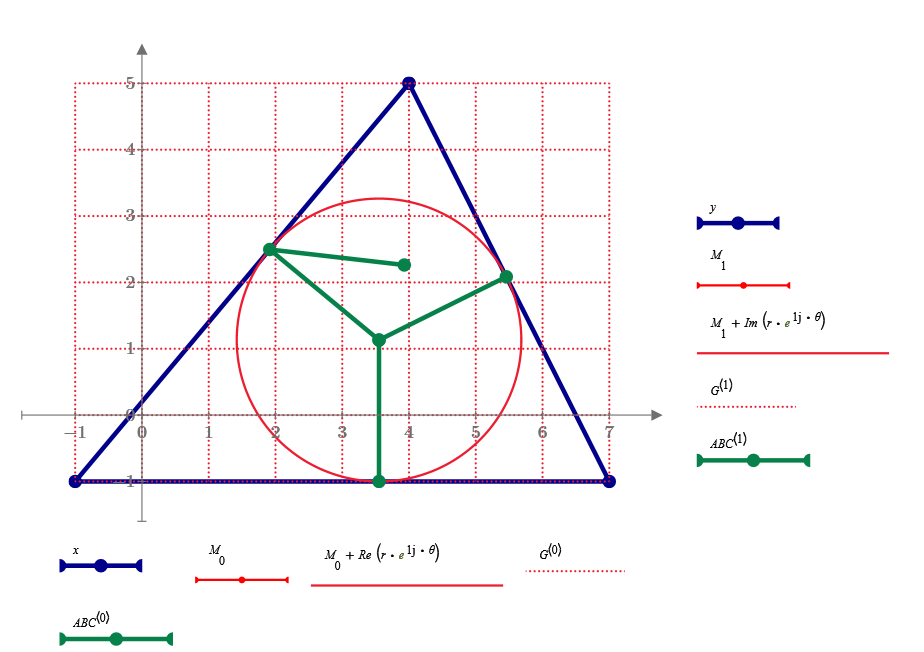
Hi,
the following video is my almost perfect animation about the triangle....:
where: C'B=C1B, C'A''=C1A2, B'C=B1C and B'A''=B1A2