- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Integrate between two functions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Integrate between two functions
So firstly sorry I’m not at home so don’t have an example to show but what I’m after is integrating an area and performing multiple tasks between two limiting functions.
I.e I have a function which I’m going to integrate underneath. this function is in terms of x. (A line that increases up the y axis as x increases)
Then I want to introduce two functions in terms of y ie vertical lines.
I then want to integrate the area under the first line and between the second two. Any idea how I do this? FYI I use prime 3
Cheers
A
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
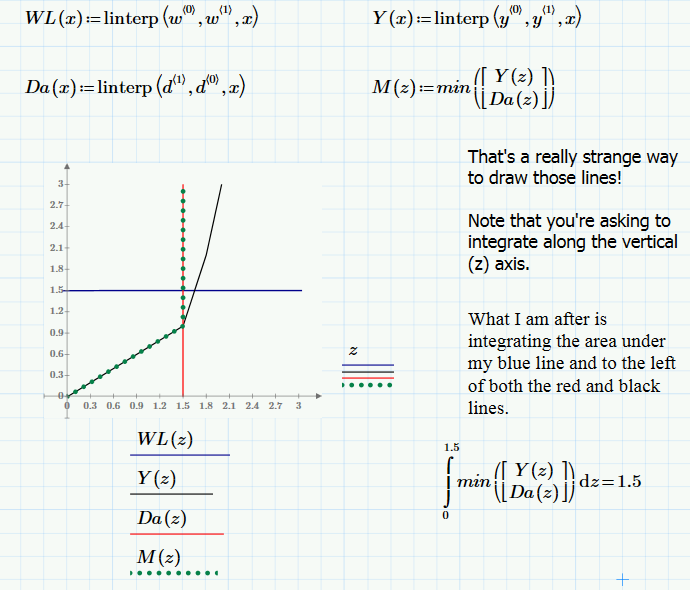
Is this what you're after?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
Thanks for that. Yes, in a way I think that gets me to where I want to be.
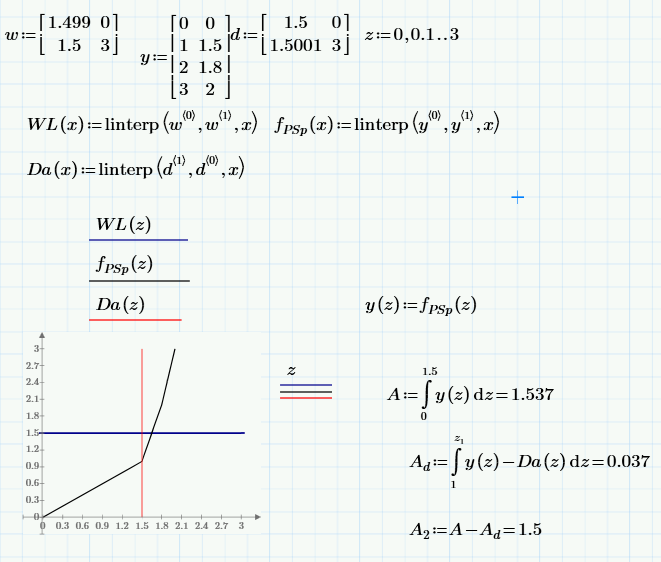
Now I am back at work, see attached image of the sort of thing I am looking at. What I am after is integrating the area under my blue line and to the left of both the red and black lines. I have experimente with a few ways of doing this and as you say can do this by taking areas away from eachother. Obviously for now I am working with simple shapes but this could get quite messy when I apply the logic to my final objective which is much more complex.
Cheers,
A
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Try this:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
Thanks for that. Yes it is not normal I agree. However, in the arena of ship calculations it is standard to integrate along the y axis for a number of reasons. In the below very simplified graph, the blue line represents the waterline, the black line the outline of half the ship and in this case the red line is a damage bulkhead which has been lost i.e. I want to find the new area of the underwater (intact) volume.
In simple terms, what does the min function do?
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"min" does just what it sounds like--accepts the minimum value
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe a better way to do this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
Thanks for that, that is magic!
That will save me allot of headaches in the future.
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
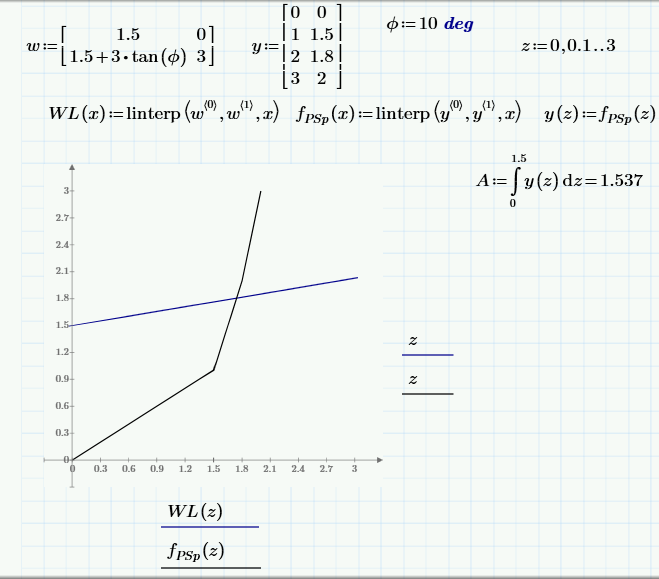
Thinking further ahead, how would you approach integrating where the upper limit is a function? In the attached, the integral only goes up to 1.5 i.e. the original waterline not the heeled line. I tried simply putting WL as the upper limit but got various error messages.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you have a second function (WL) setting the other boundary you need a double integral.
Note that the limits of the outer integration ("sea") are going to be a challenge.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator