Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Integration vertically
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Integration vertically
Hello to all,
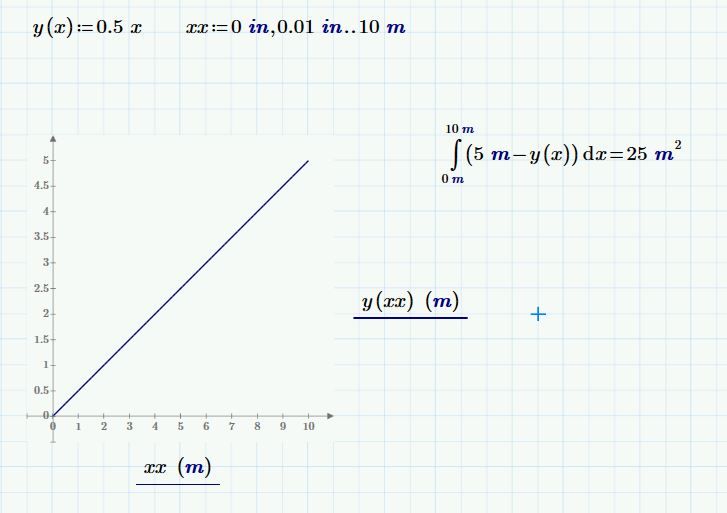
I am looking to see if you can tell MathCAD to integrate not along the x axis by along the y axis.
In the attached I am trying to integrate the area above the plotted line i.e. from 0m upward to 5m integrating all the values of x in terms of y as opposed to the default which is to integrate under the line all the values of y in terms of x. There is madness to the logic as to why I want to do this I promise.
If I can get this to work the answer should obviously be 25m^2.
Thanks
Andy
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
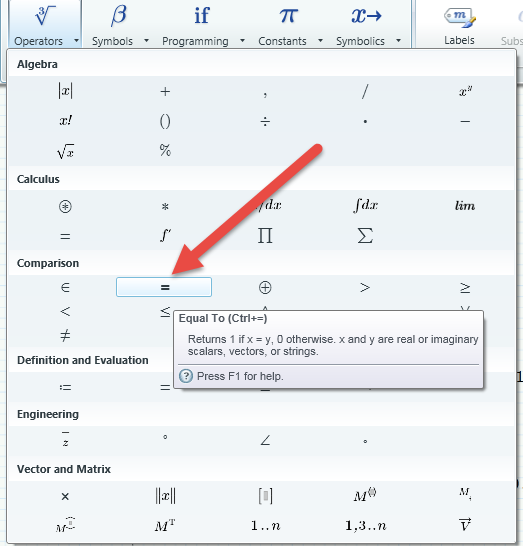
Don't blame the solver!
You used an assignment (f(x):=y) in the solve block constraint but you must use a boolean equal sign (the big fat =).
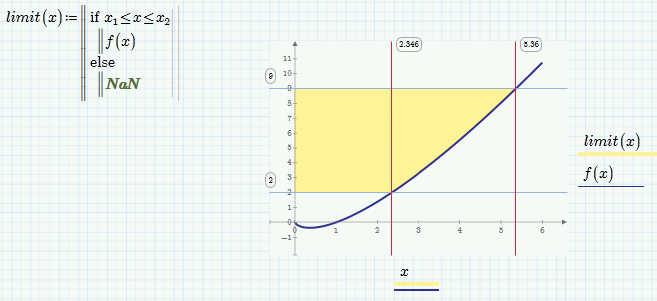
Here is an example where you can't find the inverese function in an exact analytical way.
And even when you try to find the yelllow area using integration over x, you need the inverse to find the x-limits (the same is true for your example, but there the limits where quite obvious).
The picture also shows a way to use the root function to define the inverse.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First, you need to integrate from 0 to 10 meters.
Second, your integral computes the area below the line. The area above the line is the integral of 5 - line(y)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
Yeah I know the range 0 to 5 is not going to work as it is currently integrating below the line.
So in order to integrate above the line would the integrand the same and the lower limit "line(y)"?
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're integrating along the horizontal axis!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
Yes I see that in my original example I was integrating along the horizontal axis. My question is, how would I set up the integral to integrate along the vertical axis. My issue is (connected to my other thread on defining a curve) is at the moment I am testing the theory. I will eventually be doing this with much more complicated curves.
Thanks,
Andy,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In order to "integrate vertically" you would need to define x as a function of y.. But it's been pointed out that either integration will give you the same correct answer if the problem is formulated correctly.
The only time you would need to swap integration directions would be when you have a funcction that "doubles back," has two possible values of y for the same value of x. If you can redefine that curve so that there is one value of x for each value of y, then a vertical integration would give you the answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Also why the 5m -?
If you simply integrate along the x axis the function y(x) you get the same answer?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In this simple expample with a linear function you have a couple of choices and one of the easiest sure is to stay integrating over x and simply integrate the function 5-y(x) fron x=0 to x=10 as suggested by Fred.
If this is only an example and you intend to use a more complicated function, this appraoch may work, too.
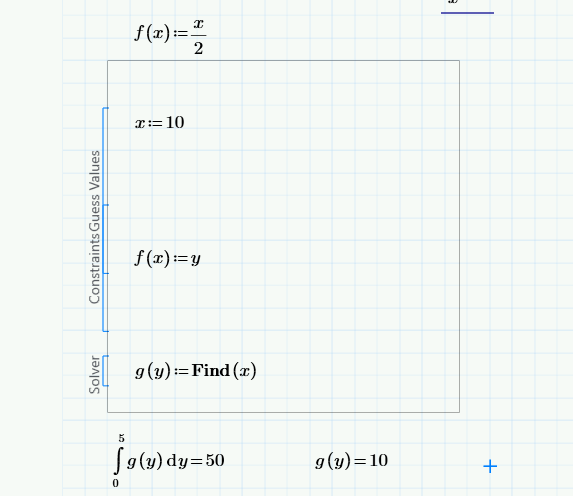
Another approach would be to find the inverse of your function (you may use a solve block to define the inverse function) and really integrate this fucntion over y.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner,
Any chance you can show me how you would approach that with this example?
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here you are:
Your function should better be injective for this to work 😉
EDIT: In the first place I had used a pic with an assignment := instead of the correct Boolean =.
To avoid confusion I just replaced the pic.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I see that that yeilds the correct outcome but not sure I follow the solve block.
Why is the guess value of x 5?
I get that the function of the line in terms of y is half of x as when x is 10, y is 5.
So that is logical that the function for is x/2.
But I am lost when you get to the guess value and constraint also why the new function g is to find x?
Sorry for being dim witted...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its overkill to find the inverse of a linear function using a solve block. I was just demonstrating this assuming you may want to use a more complicated function later.
I have chosen 5 as guess as ist the center of the interval we a dealing with. In case of this simple function an any value will do OK.
The inverse function which I call g is a function which assigns a given value of y the appropriate value of x so that f(x)=y. thats exactly what the constraint in the solve block says.
in case of your linear function f: y=x/2 the inverse of course is g: x=2*y.
We sure would not need a solve block for this 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I totally agree with that and see that if you indeed define the graph in the inverse I actually get what I am after i.e. the x axis has to be the function. Think that is the underlying anwer I wanted.
What I am really intrigued by is the solve block approach which when tested I am not sure of.
If you change the guess value this puts the whole thing off and if you recall g(y) it gives a constant of the guess value?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I feel like the solver should be being asked to find the inverse of x not x?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Don't blame the solver!
You used an assignment (f(x):=y) in the solve block constraint but you must use a boolean equal sign (the big fat =).
Here is an example where you can't find the inverese function in an exact analytical way.
And even when you try to find the yelllow area using integration over x, you need the inverse to find the x-limits (the same is true for your example, but there the limits where quite obvious).
The picture also shows a way to use the root function to define the inverse.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Also how did you shade specific parts of the graph?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, I didnt realize that I posted that error in the first place until I sent my last answer. Then I edited it accordingly 😉
The 9 (y=9) is the top limit of the shaded area in my example (its was y=5 in yours). Integration over x would give me just the area below the curve, butr we want the area between y=9 and y=f(x), so we need to integrate the difference of the two.
You can write your own shading or hatching routines in Prime, but I simply edited the screenshot using the fill tool my capture program provides.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Taking this a step further, you have obviously, skillfully used the solve block to get the inverse of the function. Can you then display the inverse function so that you can see what it is?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My mind is obviously running away with me here but I'm interested as to why Find x is the solver for g(y)?
We have initially given the function of x as a halving routine i.e. any calu of x is halved.
Then we define the function f(x) as y such that y is the halving function.
We then create a new g function which is of y that is to say the function g is actually the function f(x) ? But we are asigning g(y) to find x?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
My mind is obviously running away with me here but I'm interested as to why Find x is the solver for g(y)?
Maybe you are used to day that for the inverse function you have to switch x and y and then solve for y.
I simply omitted the switch and just solved for x.
You can formulate the solve block also lke this
Guess: y=5m
f(y) = x
g(x) = Find (y)
The name of formal function arguments don't matter. You may also use
Guess: a=5m
f(b) = a
g(a) = Find (b)
and it would work the very same way 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess I am interested to understand how the ommission of the switch and solving for x works.
I think it is just something I have to accept.
As you originally pointed out: y(x)=x/2 is x(y)=2y as y(x)*2=x and switchig gives x(y)=2y
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
I guess I am interested to understand how the ommission of the switch and solving for x works.
I think it is just something I have to accept.
As you originally pointed out: y(x)=x/2 is x(y)=2y as y(x)*2=x and switchig gives x(y)=2y
Yes - und to get answer for x(??)= you habe to solve the orginal equation y=x/2 for x, thats the reason for th Find(x).
You may as well switch x and y, then you would provide a value for x in y(??)= and are looking for the y value. Same game, just different variable names.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
Taking this a step further, you have obviously, skillfully used the solve block to get the inverse of the function. Can you then display the inverse function so that you can see what it is?
You can plot g like any other function, but as a solve block or also the root function just is using numerical methods, you can't get an analytical function term.
You would have to use the symbolics to achieve that. But with my example f(x)=x*ln(x) there is no analytical expression for the inverse - it cannot be shown using standard math functions and so consequently the symbolics fails. As you can see in the last line its still able to provide numerical values for specific values of y.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
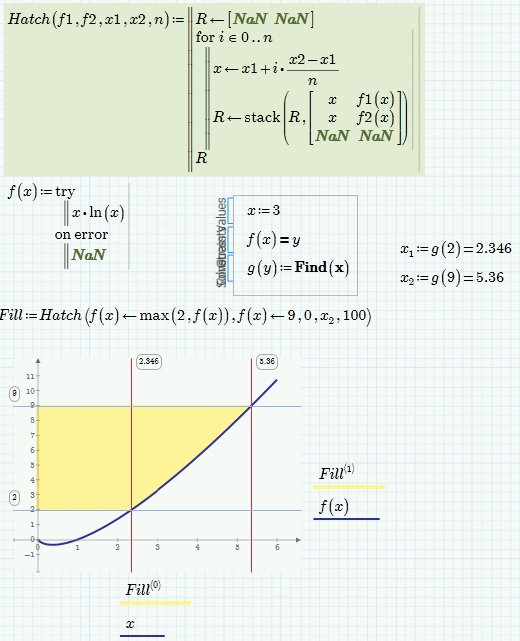
Werner, I'm curious how you shaded the graph. I have some experience in this but can't do what you did. I can't get a Bar Trace to work between two Y values. And I can plot lots of dots into the necessary area - but I have to add a routine and additional traces to the plot - which it doesn't look like you did. So, you've stumped me.
Thanks,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@dferry wrote:
Werner, I'm curious how you shaded the graph.
I am sad that I will have to disappoint you. While there are quite some ways to program a hatch or fill function to simulate a shading between two curves (usually by creating a lot of more or less narrow spaced vertical line segments, basically the output will be an n x 2 matrix) in this case I simply used the painting capabilities of my screenshot software to fill the areas in yellow 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the reply. In case anyone else is curious, the best technique I found for this case is as follows. Plot a 2nd graph (over a range of x_1 to x_2) and change the plot type to Bar Trace.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@dferry wrote:
Werner, I'm curious how you shaded the graph. I have some experience in this but can't do what you did. I can't get a Bar Trace to work between two Y values. And I can plot lots of dots into the necessary area - but I have to add a routine and additional traces to the plot - which it doesn't look like you did.
Better than dots are lines, I think (less data but better fill).
In case of the plot in question the yellow shading could also be done using Primes horizontal bars plot:
But of course both mean an additional trace.
Here is the version with the bars:
and here a more general routine which can hatch/shade an area between to graphs in a given interval:
EDIT: Just see that in the meantime you had posted your version of the shading with bars using range variables to limit the plot instead of a new function like I did.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@WernerExinger wrote:
Here you are:
Your function should better be injective for this to work 😉
I was copying you! But many thanks for the immense detail and continued support. Makes far more sense with the visual!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
I was copying you!
Ooops!! My fault, sorry! So I just had luck using the "right" guess 😉
Never a good idea to copy me, I guess.
As already written you have to use the boolean equal sign hier (but you probably had found out yourself in the meantime!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes I know that now. The point I was making was in your first post you used the :=
One thing I am intrigued by is why the 9-f(x) in the integrand like Fred did in the first example of 5-y(x)?