Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Integration with infinite upper and/or lower bound
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Integration with infinite upper and/or lower bound
Hi,
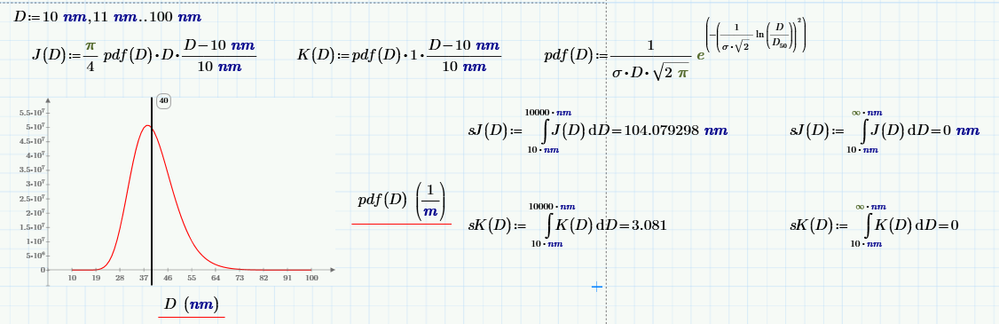
During integration with infinite upper bound, I found that the result makes me doubtful.
Then I checked it by changing the infinite upper bound with a large enough number compare to other numbers in the equation. I got a more sensible result.
my question:
1. when should we not use this infinite bounds?
2. did I miss something here in my worksheet?
- Labels:
-
Mathcad Usage
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
2. did I miss something here in my worksheet?
You did not attach your worksheet!
What happens if you delete (or move down below the calculations) the definiton of the range for D. You only need it for plotting and not for the calculations.
Are you aware that your functions J and K do NOT use the function pdf you defined afterwards but a (probably different?) function you defined earlier?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry I forgot to attached it. I edited my post.
In the previous page, there is the pdf written already.
I copied it there just to have in during screenshot.
I will try to delete D.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The D range is not the problem.
As I had shown with the screenshot from real Mathcad the problem seems to be that the wrong algorithm is automatically chosen (you cannot chose it manually in Prime) if the upper limit is not infinity but infinity times unit nm.
So here is a workaround:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is the worksheet with the built-in workaround as explained above.
As its in Prime 5 format i also attach a pdf-print of it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Apart from Werner's correct remarks, the difference is most probably due to an overflow during the numeric integration. This overflow does not occur in the range from 10 to 1000 nm, but somewhere in the vast range between 1000 nm and infinity...
Try to evaluate your integrals (which, by the way are NOT functions of D) symbolically and see what happens.
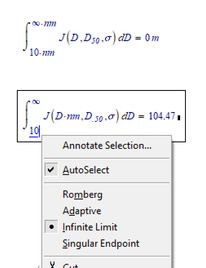
Producing a 0 answer as a result of this is bad. I'd consider it a bug.
This bug is very old, because it also appears in Mathcad 11...![]()
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In real Mathcad we can chose the algorithm used for integration resp. we see which algorithm Mathcad choses automatically.
For an infinite limit the appropriate algorithm must be used (not the ordinary Romberg) but as it seems infinity time unit is not seen as an infinite limit and so the wrong algorithm is chosen:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes, I am aware of that thing regarding the integration method/algorithm.
It is found in matlab as well.
I cannot find the way to change it here. I thought Mathcad will choose the correct one automatically until I come cross with this problem.
where can I find the menu to choose this integration algorithm in prime4?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I found that I need to pick specific range of integration by seeing the function first where its value is relevant (large enough).
The integration is done with respect (w.r.t.) to D and I also need to see the influence of w.
I put w before (in the 1st page of my worksheet).