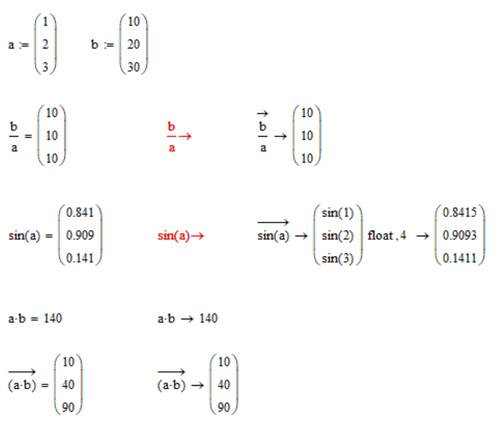Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Inverse issue?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is simply the 'inverse' of each element of your vector (so vectorization is implicit here). That's the only way way Mathcad can produce an answer that is not an error message.
The help on Matrix inverse is:
Matrix Inverse Operator
Keystroke: ^-1
This returns the inverse of a matrix. If M does not have an inverse, you'll see an appropriate error message.
Operands:
-
M is a square matrix having an inverse.
Your multiplication A * A^-1 results in 3, because A has three elements.
The symbolic (Maple) processor complains that the matrix should be square...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
It is wrong to define the matrix operator with square brackets. not [A] but simply A - although it is possible - and many ancient texts define it with square brackets. The inverse of a vector makes no sense.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There's nothing wrong about that. It's the OP's method of marking matrices and vectors.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is simply the 'inverse' of each element of your vector (so vectorization is implicit here). That's the only way way Mathcad can produce an answer that is not an error message.
The help on Matrix inverse is:
Matrix Inverse Operator
Keystroke: ^-1
This returns the inverse of a matrix. If M does not have an inverse, you'll see an appropriate error message.
Operands:
-
M is a square matrix having an inverse.
Your multiplication A * A^-1 results in 3, because A has three elements.
The symbolic (Maple) processor complains that the matrix should be square...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ifomenko wrote:
Thanks, but it's wrong behavior
Yes, from a math point of view we would expect an error message instead of a result.
To be able to interpret the result we have to know, that Mathcad will switch into automatic (implicit) vectorization whenever the operation will make no mathematical sense when applied to vector or matrices.
Many people find Mathcads implicit vectorization quite convenient but personally I'd prefer to explicitly use vectorization even though Mathcad would apply it implicitly on its own.
As you can see in the screenshot, the symbolic processor is more strict and requires explicit vectorization: