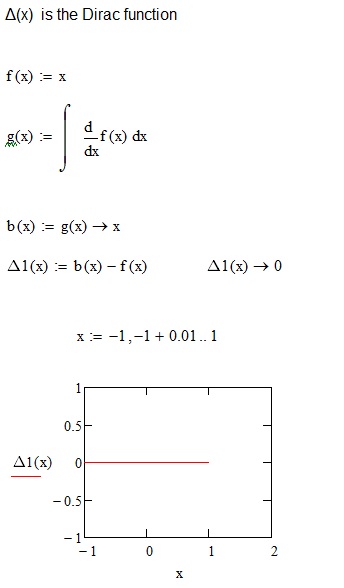Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Is there a reason for : "All evaluations resulted in either an error or a complex result." ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is there a reason for : "All evaluations resulted in either an error or a complex result." ?
Hello, Everyone.
Is there a reason for : "All evaluations resulted in either an error or a complex result." ?
Regards.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello, Loi Le
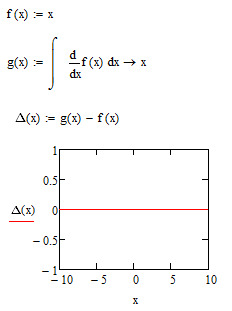
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks, Viktor. ![]() . And I still have a small query:
. And I still have a small query:
Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

OMG, after all those questions you posed in that forum, and all the answers you got, do you still believe, that the following equation is correct
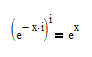
or do you really still believe that Mathcad is capable of handling those ambiguities correctly and is a suitable tool to deal with that kind of calculations?
The equation is NOT correct (its missing an infinite number of "solutions"
-> 
and Mathcad sure is NOT a tool which deals with that kind of calculations in a satisfactory way.
You must accept those facts at last!!
All the following results are correct, but Mathcad is picking just one of the infinite number of possible correct results. Finally thats (again!) the reason for your "problem". You won't get a real result from your integral if Mathcad picks the "wrong" (in fact its not wrong) value.

So calculate your integral yourself by hand, replace i*x in the exponent by i*(x+k*2 pi) and see where you get.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I greatly appreciate your spending time for my question, Werner. ![]()
![]()
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, X-Mas is near and so you should get a "solution" for your specific "problem". Keep in mind that this solution might not apply to other similar "problems".
In your case adding a constant (you may see it as a constant of integration) does the job pretty well, but in other cases you probably would need to add a different constant depending on the value of x because Mathcad is choosing different (all correct) solutions from the infinite number depending on x as explained above.
So its not a solution, just a cosmetic to make you happy 😉
BTW, it seems to be your destiny to run into problems with ambiguities. While most of the time you struggle with the ambiguity when dealing with complex numbers, this time its (additionally) the ambiguity of the indefinite integral which again has an infinite number of "solutions".

Merry Christmas!
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator