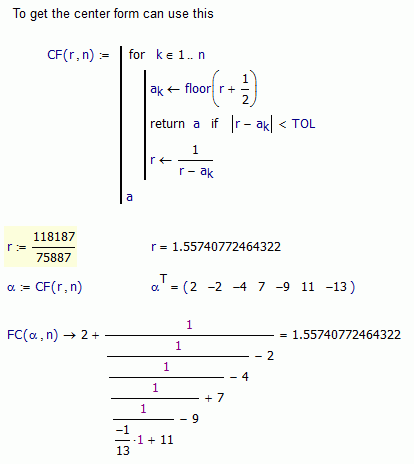- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Is there a way to transform the continued fraction ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is there a way to transform the continued fraction ?
Hello, Everyone.
Is there a way to transform LHS to RHS ?
Thanks in advance for your time and help.
Regards.
Message was edited by: Loi Le
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh, I forgot to tell that you must to provide the transformation sequence ci for get the generalized from the canonical expansion. If not, there are a lot of chances to get any sequence. The canonical is unique, the generalized not.
Hope this helps.
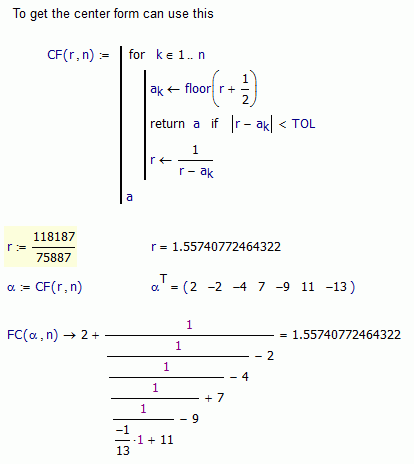
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
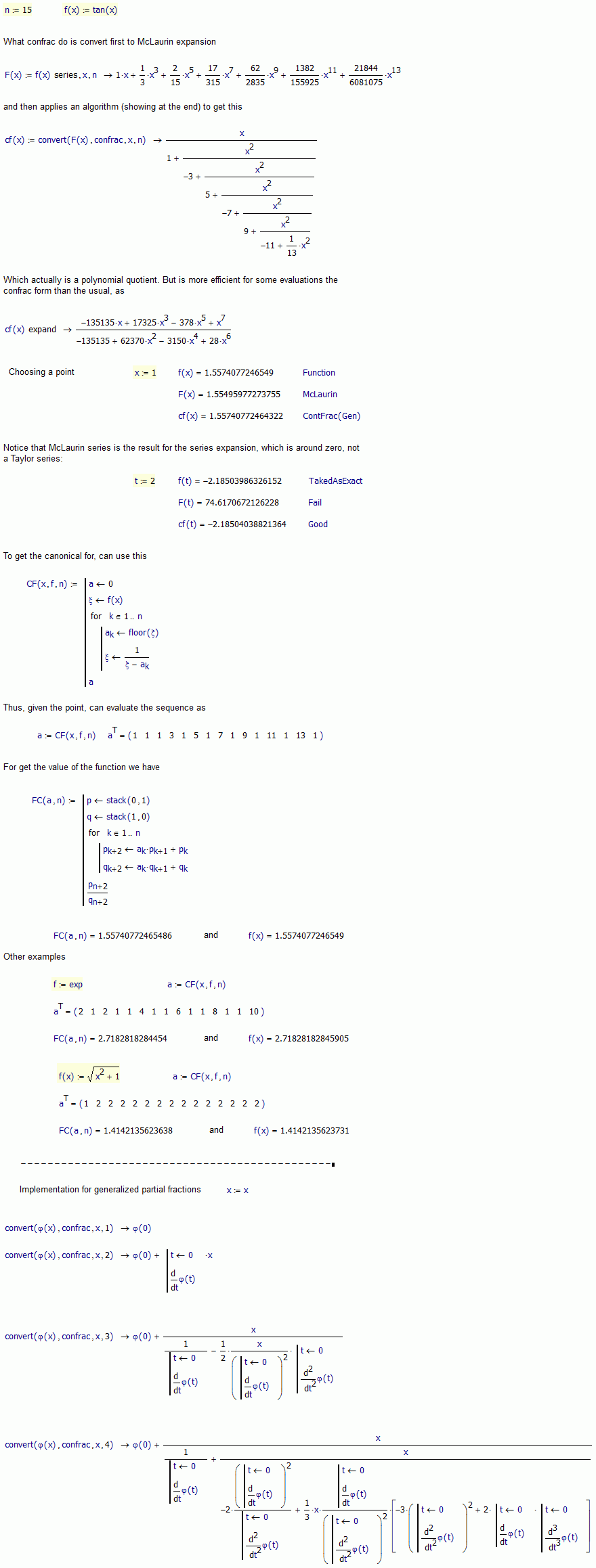
Sure. By a theorem. First, notice that RHS isn't a continued fraction, is a generalized one. What you show is a special case of the equivalence transformation, making ci=1. See Generalized continued fraction - Wikipedia, the free encyclopedia
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm sorry, my question should be :
How to make a change from the continued fraction to the generalized continued fraction ?
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I greatly appreciate your time and help, Alvaro. ![]()
![]() And I have a similar question is :
And I have a similar question is :
Is it possible to create a program function with the input and output like as the above or a similar ?
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yep. Here it is. I know that in prime there are a function for hidding symbolics values, but don't remember which.
Best regards.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh, I forgot to tell that you must to provide the transformation sequence ci for get the generalized from the canonical expansion. If not, there are a lot of chances to get any sequence. The canonical is unique, the generalized not.
Hope this helps.