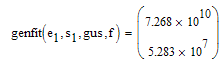Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Least Squares Fit does not compute
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Least Squares Fit does not compute
Hello folks,
does anybody understand why this leastsquaresfit does not compute for this plain problem?
Thanks in advance
Raiko
p.S.
I'm using Mathcad 15 M045 on a Win 7 machine.
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's a scaling problem. I would expect changing TOL or CTOL would fix it (this would work for genfit or minerr), but it seems that does not work.
Your guess value for the slope was also a long way off.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's a scaling problem. I would expect changing TOL or CTOL would fix it (this would work for genfit or minerr), but it seems that does not work.
Your guess value for the slope was also a long way off.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well yes, the guess values where indeed far off, however I've had success with even wilder guess values for linear problems.
Thanks
Raiko
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, the guess value was not the fundamental problem. That was just an additional observation ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's a possible way to automate the scaling and rescaling. It should also not be necessary to deal with "UntisOf" because "mean" would take care of the units.
Is there a better, shorter way to do the rescaling?
We have to multiply the whole 2 x 3 marix with mean(s.1) (which is easy to achieve) and then only the first row has to be divided by mean(e.1).
EDIT: I just notice that the rescaling of coeff needs a unit strip off, which should be easy to accomplish. The reason ist that we cannot have different dimensions in a matrix, which would be the case, if e.1 is not dimensionless.
Its interesting that "line", which also should use a least square fit, I guess, dies not show this scaling problem.
Regards, Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its interesting that "line", which also should use a least square fit, I guess, dies not show this scaling problem.
But it's a linear least squares fit, so there is no iterative process. It just does some matrix algebra.
minerr etc do suffer from similar scaling problems (although I have not tried this specific data set) because CTOL is an absolute number, not a relative one. So if your numbers are like these, around 10^8, a convergence tolerance of 10^-3 is one part in 10^11. It would be much better if the convergence criterion were relative, so 10^-3 meant that the chi-square changed by less than one part in 10^3.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
Its interesting that "line", which also should use a least square fit, I guess, dies not show this scaling problem.
But it's a linear least squares fit, so there is no iterative process. It just does some matrix algebra.
Sure, of course you are right. Shame on me 😞
But what about genfit - which algorithm is used here?

Don't think that genfit "realises" that f is linear.
> It would be much better if the convergence criterion were relative
But relative to which value?
Its something I tried to achieve in the approach in my next post, but I can think of situations where this approach will fail, too.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But what about genfit - which algorithm is used here?
Don't think that genfit "realises" that f is linear.
Genfit uses LM, only. I've not noticed scaling issues with genfit, but I almost never use it because minerr is more flexible. It uses the same algorithm though, so I would also expect it to show scaling problems in some cases. It's a different algorithm to LeastSquares, so the scaling problems are not likely to be exactly the same for the two functions.
> It would be much better if the convergence criterion were relative
But relative to which value?
Not to any of the parameter values, but to the chi-square, i.e. the RMS residual. I believe that's what CTOL is compared to now (it is certainly what it should be compared to!), but in an absolute way, not a relative way. So with the default CTOL, when the chi-square is below 10^-3 it's considered to have converged. That's a problem, because the magnitude of chi-square depends on the magnitude of the data. I've seen cases where it doesn't converge (very large magnitude data), and cases where it just gives a garbage fit (very small magnitude data). They can be fixed by changing CTOL, but that wouldn't be necessary if CTOL was compared to the relative change in chi-square, rather than to chi-square itself.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I dont't think that making the accurcy dependend on the relative change of the RMS residuals compared to CTOL will solve all scaling problems we encounter. It will deal with the problems we may have with too large or too small Y-values but will not consider the magnitude of the X-values, which may be responsible for some nast effects, too.
I just wonderer, like you, why changing CTOL (or TOL, I am not always sure which one applies, but here it should be CTOL, I guess) does not effect the outcome here.
In the help (yes sometimes I'm really reding help files) I found that LeastSquaresFit has an optional parameter for convergence accuracy. And obviously for the default value the routine has a value hardcoded and does not look for CTOL.
An accuracy of 0.5 (instead of the default value of ???) does the job in this case.
But multiplying the X-values by 10 (brings them from around 10^-3 in the area of 10^-2) makes the routine fail again until accurycy is set to 1.05. Hmmm!

Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sure, changing the behavior of CTOL would not fix all scaling problems, but it would at least fix some. Regress used to have a serious scaling problem with x-values, because the higher powers of large numbers would blow up. Mathsoft fixed that one (after some prompting ![]() ). They were also willing to make that fix more general for minerr, etc, but nobody could figure out how to automatically handle x scaling for arbitrary functions. There are some very old threads somewhere on the subject.
). They were also willing to make that fix more general for minerr, etc, but nobody could figure out how to automatically handle x scaling for arbitrary functions. There are some very old threads somewhere on the subject.
I hadn't noticed that LeastSquares has it's own tolerance parameter, and therefore it ignores CTOL. I guess reading the help really does help sometimes ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is the modified sheet using an allpurpose, unit-aware LeastSquareFit routine which also should not show those scaling problems.
I just noticed that I never changed your original guess vector. It really seems not to matter that its way off.
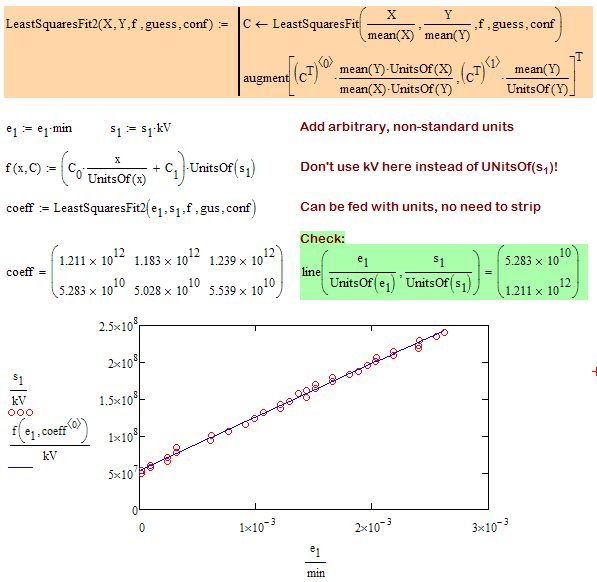
Regards, Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner,
neat function!
Raiko