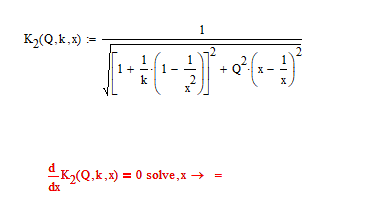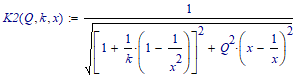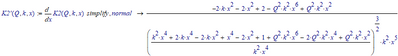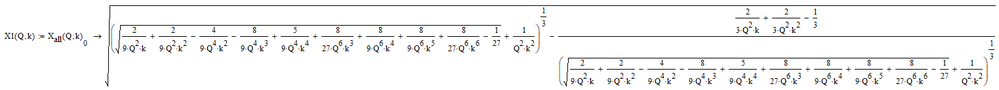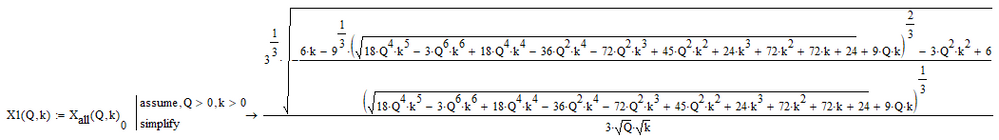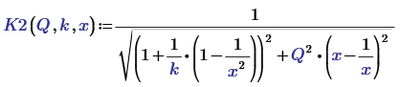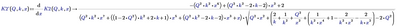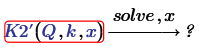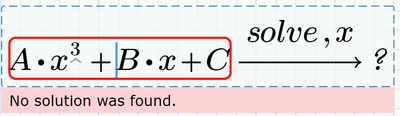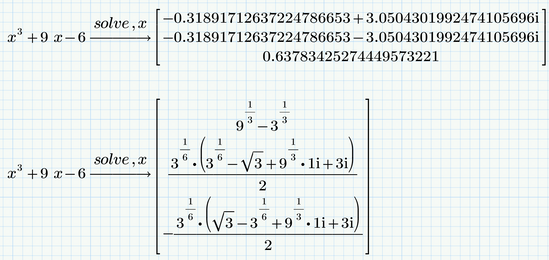Math equation solving problem

[J_power]

Hi experts,

Can anyone know how to solve this problem?

it seems the equation is too complicated, so the system can't solve it.

any other methods that can solve this issue?

[Werner_E]

You sure should attach your worksheet, not just show a pic.

What is the error message you get?

Has the variable x not been assigned a value before anyway? If you did, that would throw an error.

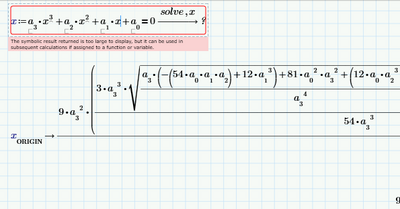
On first sight you may end up with a biquadratic equation of sixth order. Its quite possible that Mathcad either is not able to solve it symbolically or (more like, I guess), that the solution Mathcad can come up with is too large and cannot be displayed. In the latter case you still can assign the solution to a function in Q and k and use that function in later calculations.
It may also be the case that Mathcad is not able to display the full solution vector (I assume a 6 x 1 vector) but is able to display all or most of its entries singly one by one.

You may also parametrize a solve or a root call so you can create a (numerical) function in Q an k.

So there a quite some possibilities to deal with the problem. While it might be possible to let Mathcad show you the symbolic solution (at least the one with a positive, real value which as I guess is what you are interested in), its highly likely, that you don't really need the symbolic expression.

Are you sure that you really need a symbolic solution? If Q and k are known, you may try a solve block or the root function as well. After all you followed the symbolic solve by a numeric equal sign. If Q and/or k are unknowns, this would yield an error in any case.

[terryhendicott]

Hi,

The error message states make a function

So turn it into a function then use the function

[Werner_E]

Your function K.3 does not need the third argument x as x is the variable which the expression is solved for and so should not appear at the (too large) solve expression.

In another thread I got the impression that the OP was only interested in real and positive solutions. In the symbolic symbolic solve vector

this seems to be the very first entry. Wen can isolate it and Mathcad even is able to display it

"simplify" doesn't do a great job on this

But as I guess that Q and k will only take real values, we can talk Mathcad into simplifying the expression a bit further

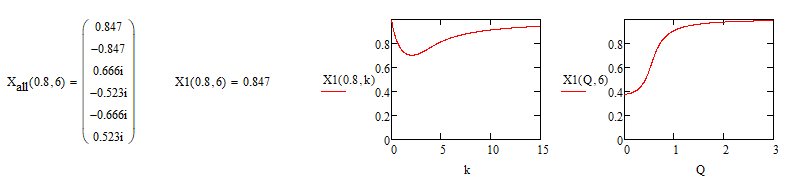
Now this function can be used numerically at will

I can be proven wrong but I still think that a pure numerical approach without using the symbolic "solve"  would be more appropriate.

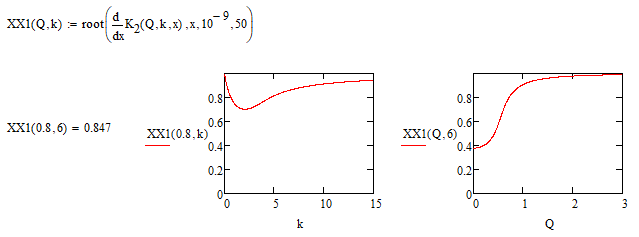
Maybe like this:

[LucMeekes · Accepted solution]

Then:

and:

Success!
Luc

[Werner_E]

Nice! 👿

Maybe it should be explained to @J_power  that you are using Mathcad 11 and MC11 is able (or could be made able) to display larger symbolic results.

[LucMeekes]

Incidentally...Prime 8:

(No solution was found).

Luc

[J_power]

Hi @LucMeekes ,

Did you sue Prime 8 to do that?

[LucMeekes]

I used Prime 8 to check that. As shown, its symbolics isn't as powerfull as that of Mupad, or Maple.

Success!
Luc

[Werner_E]

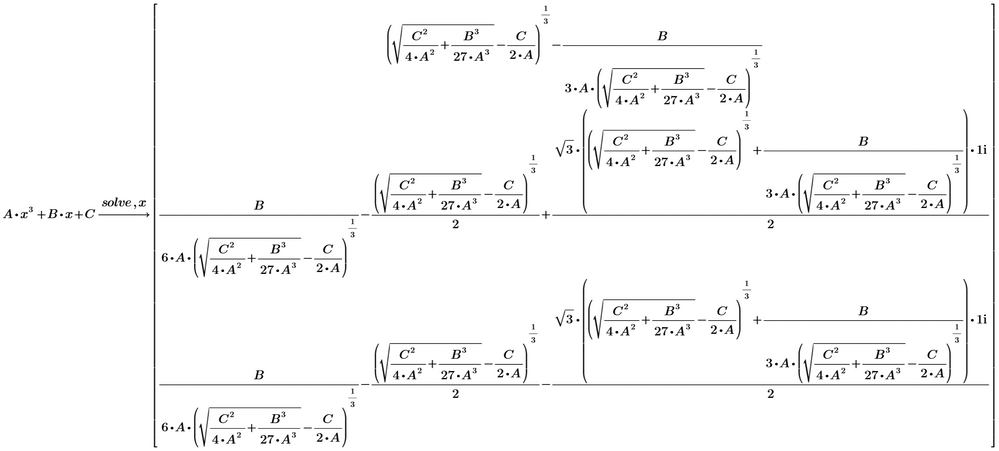
I first thought it could be once again a problem with the infamous auto-label feature, but it looks like the new symbolic in P7 and P8 is not able to solve a third order equation.

While being nasty to do so by hand, the solution is mathematically well know (Cardano) and should not be a problem for a CAS.

In P6 we can switch back to the legacy symbolics (muPad) and get this

Not extremely nice to look at, but a solution which could be used for further calcs.
BTW, if we add a summand with x^2, we get the "the solution is too large to display" warning, but at least a solution was found.

Using numbers the new engine switches much sooner into numerical approximating float mode while the old engine (muPad) still returns an exact result:

[LucMeekes]

Hmm,   Prime 7:

(Cut off at paper edge)

This is where Prime 7 quits:

Of course Mathcad11/Maple knows how to do this:

(Cut off at paper edge)

Luc