Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Mathcad 14 evaluates integration wrongly
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 14 evaluates integration wrongly
It seems that my Mathcad 14 has given me a few wrong symbolic evaluation for indefinite integrations, or at least it is different from what I worked out on paper. Or are they actually the same?
The first one I had is this:
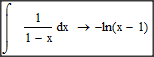
I tried to integrate this but apparent the answer is different from what I get from doing on paper. My answer is: -ln(1-x) instead of what Mathcad had given me.
The other one is this:
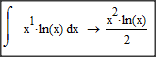
The answer I get from doing by hand is ((x^2)/2)ln(x) - (3/4)x^2
How come Mathcad gives me an evalution that looks so different from what I do manually? And is Mathcad wrong?
Thanks.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The first answer is correct within a constant of integration. Remember that (x-1) = -1*(1-x), so when doing the log of the product you have a ln(-1), which is -i.pi as a the (complex) constant of intergation. This trips up many.
The second answer isn't what I get for intergal x*ln(x) dx, or (x^1)*ln(x) - I'm using V15 M005.
Philip
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am agreement with Philip, just adding comment:
If you want to see if two answers are the same, just subtract one from the other.
In the first case, if you do symbolically, you get 1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you want to see if two answers are the same, just subtract one from the other.
In the first case, if you do symbolically, you get 1.
This would surprise me, as the difference should be i*pi or -i*pi (the ln(-1) that is). You have to assume x>1 or x<1 to get Mathcad to simplify it that way.
Concerning the second integral it seems, that the "3" in Ken'smanual solution is a mistake and should be a "1"
The solution he tells us he is getting from Mathcad I can only duplicate, if I format the "x" in "ln(x)" in a different style (not "Variable"). Then "ln(x)" is treated as a constant factor.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Winfrod wrote:
Concerning the second integral it seems, that the "3" in Ken'smanual solution is a mistake and should be a "1"
The solution he tells us he is getting from Mathcad I can only duplicate, if I format the "x" in "ln(x)" in a different style (not "Variable"). Then "ln(x)" is treated as a constant factor.
It is good to see an explanation and a method of replication of the 'fault'.
The cases where the variable style changes can be tricky!
I'm guessing that the variable/constant style swap was the problem. In the newer veresions you can end up with variables that are in constant style (or is that vice versa). This is more obvious if you apply colour to the style. I use a soft brown for constants, which makes it more visible when the initial typing produces such 'mistakes'.
Philip
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Apparently, the "x" in the ln(x) is set as a variable style in my evaluation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What is the style of the other x's?





