Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Mathcad 15 "onefn" function problems
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 15 "onefn" function problems
I am having trouble with the onefn function in Mathcad 15. I get double entries in the 1/f noise vector and if I take the CFFT(ofn) I get a zero as the first result. Also I do not understand the mirrored magnitude plot of the 1/f Noise. I also don’t understand why the range variable even starts at zero. That would give infinity for 1/f. See attached.
Bill
Bill Dumke, RF Engineer
Nsight Telservices dba Cellcom
450 Security Blvd
Green Bay, WI 54313
Solved! Go to Solution.
- Labels:
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry. Because of where you put the comment I was looking at the wrong thing! Yes, you are correct about the double entries. That must be a bug in the onefn function. Here's a fix.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am having trouble with the onefn function in Mathcad 15. I get double entries in the 1/f noise vector
You mean they are complex. Yes, that is a property of the Fourier transform. The FT of a perfectly symmetric function, for example cos(x) is real. The FT of a perfectly asymmetric function, for example sin(x), is imaginary. In general the result of a FT is therefore complex. The magnitude of the signal is the square root of the sum of the squares of the imaginary and real parts, and the phase is the arctan(imaginary/real). So the magnitudes of cos(x) and sin(x) are the same, but the phases differ by 180 degrees.
if I take the CFFT(ofn) I get a zero as the first result.
The result of a FFT always starts at zero frequency, i.e. DC. You subtracted the mean of ofn, so the DC component is zero.
I also don’t understand why the range variable even starts at zero. That would give infinity for 1/f. See attached.
The result of an FFT always goes from zero frequency to some upper limit. Yes, that would result in 1/f being infinite, but the concept of 1/f noise becomes meaningless when f=0. To measure one period of anything with truly zero frequency would take an infinite amount of time. Even very low frequencies have no real meaning for most applications. If you are measuring the period of sunspot activity a period of 1 year has real meaning, but if you are building an RF circuit (an example deliberately chosen because that's your speciality!) a period of 1 year has no practical meaning whatsoever.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
Thanks for the reply.
No, they are not complex. Just two rows each of the same real number in the vector. This holds for the entire 1/f vector. I have never seen anything like this.
I have attached a pdf file so you can see the onefn output with Mathcad 15.
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry. Because of where you put the comment I was looking at the wrong thing! Yes, you are correct about the double entries. That must be a bug in the onefn function. Here's a fix.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
Thanks for the fix. And thanks for the answers on the other stuff as well.
Just one more question to help with my math ignorance. Why does the frequency domain plot look like a mirrored image? It looks like I am going to have to take double the time domain input points to cover a frequency range with the same number of points from 0 up to the center of the plot which I assume is the highest frequency.
Bill.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
and the phase is the arctan(imaginary/real). So the magnitudes of cos(x) and sin(x) are the same, but the phases differ by 180 degrees.
That's 90 degrees (pi/2 radians, units of Angle) ![]() not 180... I think you were thinking faster than you typed.
not 180... I think you were thinking faster than you typed.
Philip
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
90 degrees and 180 degrees are actually the same thing, because degrees are not a proper unit. I just chose a different size of degree.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
Speaking of phase, if I take the argument of ofn with or without your fix. I only get angles from 0 to pi radians, not -pi to pi as it should be. Is this another problem with the onefn function or am I thinking wrong here? See attached.
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The phase plot is correct. You are taking the phase of the time domain signal, which is real, and therfore has only two phases: zero for positive values and pi for negative values.
Just a comment on why no infinities. Regardless of the input waveform, the transforms are DFT's over a finite set of points, not infinite line, continuous FT's. The result of all the various DFT's will always be finite (but a large DC offset can lead to numerical inaccuracies if the dynamic range is pushed).
The CFFT gives a spectrum vector starting at f=0 to f= (almost) fs, the sampling frequency. The Nyquist freq.fN is in the middle, and the upper half of the spectrum is just a repeat (remember - the DFT is periodic) of the spectrum from -fN to f=0. For real signals time, this gives the conjugate symmetry of the spectrum. This symmetry doesn't exist for complex signals. In fact, when one constructs an 'analytic' signal, the upper half of the spectrum [f = (-fN,0) or (fN,fs) - take your pick] is zero.
Hope this helps.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Lou,
Thank you very much for the reply.
I included the fixes and info in the attached file.
I am working with a baseband signal in the frequency domain, from 0 to n. The time domain representation of this signal has the same number of points, 0 to n.
So how do I use the onefn function to get rid of the symmetry in the frequency domain?
(The 1/f noise should decrease with n over the entire frequency domain.)
Thanks for your help.
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The simple answer is that you can't. The symmetry is inherent from the fact that you have a real time signal with a spectrum that is conjugate symmetric. If you have 1000 time samples at 1ms sample period, then fs = 1kHz, and fN (Nyquist) = 500 Hz. The DFT of these real samples is only uniquey defined over the Nyquist bandwidth (say from f=0 to f=fN). In fact, given that the samples represent a baseband signal, they define a spectrum in the freq. range f= -500 Hz to f= +500 Hz, which is periodic in freq. Thus, any 1 kHz band spec suffices.
When you compute the CFFT (my favorite DFT), it will return 1000 points, spanning a freq range from f=0Hz to f=999Hz in 1 Hz increments (not -500 Hz to +500 Hz). The spectral value at f=990 Hz is equal to the spectral value at f= -10 Hz and equals the complex conjugate of the spectral value at f= +10 Hz, etc. The freq spectrum gives the 1kHz periodic spectrum with the freq origin as the first point, not in the center, as typically illustrated with continuous time, double-sided spectra. The information you want all resides in the lower half of the spectrum, so you can just use the band 0 to fN. then your graphs will look like what you expect.
Some additional comments. The power spectral density is proprtional to the squared magnitude of the DFT, not the DFT, and typically has a large variance requiring smoothing, if starting with a random time domain signal.
Phase noise is not the random phase of the DFT. Rather, it is the power spectral density of the time domain signal with the amplitude variation of the envelope removed - a completely different animal.
Lou
P.S. I have v11 and v14, not v15 (and thus no onefn fct.), so I've fudged your sheets to use white noise as a calc. example. Doesn't give the spectral shape, but good enough to track the issues raised so far.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Lou,
The onefn function is from the signal processing e-book which comes with Mathcad 14 as well, or at least it can be downloaded for free, if I remember correctly. I don't have 14 anymore. I still have 11 which at least is always stable, and which I still use most of the time, except when I am doing simulations which require more power.
Anyway, I didn't see any attachment from you, but I would appreciate seeing it.
I saved my Mathcad 15 file as Mathcad 13 and attached it if that would help you. (I don't know if 13 had the onefn double entry problem or not. I know the signal processing e-book with Mathcad 11 works fine with onefn, no double entries.
The reason why I am using Mathcad 15 and concerned about the length of the vector is my simulation has two signal vectors, I & Q, 100,000 entries long. Every once in a while I have "out of memory" issues and it takes a long time to process. I will try doubling the length to 200,000 of the onefn function and see if it will work or not.
Thanks for all the help and explanations.
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was able to open your v15 files in my v14 (thanks to xml format?). Other than redefining some functions (onefn and mag) to produce reasonable results, everything worked out-of-the-box. Richard already addressed the double entry problem in the onefn time domain generation, so I just ignored it, and addressed the mirror spectrum and phase questions (which are distinct) - and I hope answered. I don't think the spectral shape I used (not 1/f) was critical to my points.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Lou,
Please post your file. I would like to see it. It looks like onefn will work OK with 200,000 points. Although plotting one graph has so far taken over half an hour without completing. Without seeing your file I am assuming I just use the first half of the time domain vector? (I have a feeling that is not how it works.)
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I only substituted a different fct. to generate a noisy signal. Mine is white noise, not 1/f. Otherwise, no difference in # points, sizes, etc., so the file itself is not illuminating.
The point I was making (see my 7/28 posts) is that if you start with 1000 real time samples, you will get half this number (500 in this case) of independent complex spectral points in the Discrete Fourier Trqnsform, or DFT (CFFT is one of the available DFT's). This is the sum total of all the unique info in the DFT. The other half (500 points here) of the transform is the same information rehashed (complex conjugates). That's it.
In my example of 1000pts. at 1ms (1 sec span), there is only unique freq. information from 0 to 500 Hz (first 500 points). the second half is inherently the mirror of the 1st half. The symmetry has nothing whatever to do with any properties of the onefn fct. - it is a fundamental property of the DFT. 1000 real points in; 500 independent complex points out (the mirrored second 500 giving no new info). The data you have does in fact decrease as 1/f (powerwise) over the full independent freq range of 0-500Hz.
Solution: simply drop the second half of the spectral components, and look at the 1st half. Some bookkeeping is needed to take care of the differences in sizes and indexing.
Your suspicion is correct; use the full input vector of time samples. Why generate 2k points if you then use only 1k for further calc? Only the number of points used for calc matters.
Re: plot/sheet speed, my practice is to assign new variable names to new vectors, and minimize invoking of functional calls. If you define y=CFFT(x), this calc is done once, and then you can plot, calc based on y. If you invoke the fct. call CFFT(x) instead of y, then it does another calc at that time. If it's subscripted, CFFT(x)sub n, it may do a complete vector function calc. for each subscrpt, which explodes very quickly. If I find a need to invoke the same function call more than once, I'll assign a new name to the result to avoid recalc.
Lou
P.S. I see italics, bold,... avail for formatting, but I didn't see how to make subscripts and superscripts. Is this possible here?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Lou,
Thanks for the reply. I want to make sure I understand this correctly. If I use the fixed onefn function to generate 1/f noise of 1000 points in the time domain, then I can add that to 1000 points of signal data in the time domain.
Then when I take the CFFT or whatever to get that sum of noise and signal data into the frequency domain, I will not have to worry about the frequency domain having a minimum value of 1/f noise in the middle of the spectrum? This doesn't sound right to me.
For example, if my signal data were all zeros in the time domain, then the frequency domain would have a minimum in the middle with the symmetry we discussed earlier. This would not be correct over the frequency range of my baseband signal which has the same number of points as the time domain I and Q signals that make it up. So it would seem to me I would have to do something more than just using the entire onefn time domain results.
Please let me know if I am wrong on this, or on how to do it properly.
Also the question about subscripts and superscripts, I can answer. If you are talking about text formatting, just highlight the text you want to be a subscript or superscript and select the Format menu at the top of Mathcad, choose Text and then select the subscript or superscript option. You can also use Greek characters as well just by typing CTRL G after the English character you want changed to Greek.
In terms of math regions it is more complicated. I suggest if you want to know more look in the Help menu under subscripts, math. Mathcad has a very good Help menu, although I always seem to run into error messages that are not listed there for some reason or other.
Although "literal subscripts" in a math region can be created which don't do anything except change the name of a variable. All you have to do is after you name the variable, press the period key on your keyboard and you can type in whatever you want for a subscript. You can include punctuation marks, etc. by using the CTRL SHIFT k simultaneously. You will see the cursor change from blue (math) to red (text). Then you can type in whatever punctuation mark you want. Simultaneously press the CTRL SHIFT k combination again and you will be back to the blue cursor for math where you can continue with your "defined as, :=" or whatever.. When you click on a variable with a literal subscript, the subscript will separate from the variable name a little. With range variable subscripts they will not. So you can tell the difference that way. Otherwise, they look the same.
I hope you can answer my question. Thanks, Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>If I use the fixed onefn function to generate 1/f noise of 1000 points in the time domain, then I can add that to 1000 points of signal data in the time domain.
Yes, you will then have a 1000 point vector of S+N.
>Then when I take the CFFT or whatever to get that sum of noise and signal data into the frequency domain, I will not have to worry about the frequency domain having a minimum value of 1/f noise in the middle of the spectrum? This doesn't sound right to me.
It sounds as though you expect the second half of the spectrum to give meaningful new info (such as 1/f spectrum from 500-100Hz). Wrong! there is no new information on this freq band in the DFT. Para 3& 4 of my 7-28 post address this. It gave all of the specifics and the source of the symmetry; it has nothing whatever to do with the specific function (onefn) used to generate time samples.
I think you are mixing up some basic aspects of DFT's with the specifc 1/f noise/system you are trying to model. I can't add any more to what I've already said.
Lou
P.S. My questions about subscripts and superscripts related to posting responses (such as ths one) on this forum; not within Mathcad itself.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Bill,
Glad you decided to make the plunge. It looks like the Adept site continues to have serious problems. I got a whole bunch of odd emails from some sort of support site as a result of just a couple of postings yesterday.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am logging the issue with onefn function.
Mona
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mona,
Attached is the solution to the onefn problem. I suggest the conclusion at the end be added to the Signal Processing Book Noise Generator section to eliminate confusion.
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have refrained from commenting in this thread because of a lack of time, but I have watched it (mostly).
You conclusion is not correct. The conjugate symmetry has nothing to do with the onefn function. It's a property of the Fourier transform. I don't even follow some of your reasonaing. You generate a noise vector, "ofn", with 2000 points. Then later down the worksheet you chop this noise vector in half to get TimeDext, declaring that this new vector has the "correct" number of points. Why do you think that cutting off the second half of "ofn" results in a noise vector that is any more or less "correct" than "ofn" itself?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
The problem is that it is easy to assume, as I did, that the noise generated by onefn can be used as additive noise in the time domain. It cannot. The correct "physical" 1/f noise can only occur if only the first half of the frequency domain is used. Any number of points of onefn noise will produce conjugate symmetry about the midpoint, so it cannot be used as additive noise with a real signal.
I am talking reality here. I am working with a baseband signal in my system. Taking the fft of the baseband signal with the onefn noise added to the signal produces the same symmetry in the frequency domain, which is not reality! In the real world, no pun intended, 1/f noise falls off forever with frequency. It doesn't matter whether the fft causes it or not. So the only way the onefn function can be used is by taking the fft, extracting the first half and adding it in the frequency domain.
You are thinking math and ignoring the reality of physics..
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You are thinking math and ignoring the reality of physics..
I understand both the math and the physics. It seems you misunderstand the math though.
Any number of points of onefn noise will produce conjugate symmetry about the midpoint,
Forget onefn. Any number of points of any real (i.e. not complex) signal will produce conjugate symmetry in the output of cfft or CFFT. It's a property of the algorithm and tells you nothing whatsoever about the signal except that it's real.
Taking the fft of the baseband signal with the onefn noise added to the signal produces the same symmetry in the frequency domain, which is not reality!
You are correct, it's not reality. The second "half" (although it's not exactly half) is there for good mathematical reasons (and if you want to subsequently use icfft it is neccessary). It is not there because it tells you anything about the physics. A Lou already said, just throw it away. What you are left with describes the physics.
To be exact about it, the second half of the frequency vector is the reverse of the complex conjugate of the first half, with the exception of either 1 or 2 points. If the number of points is odd, then point 0 is unique. If the number of points is even then points 0 and ceil(last(freq)/2) are unique. This will recover all the independent points:
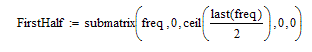
Just ignore the others.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
Now you have it. That is basically what I had to do. It cannot be done in the time domain. The extracted 1/f noise has to be added in the frequency domain. But I believe that this should be noted in the Mathcad Signal Processing e-book, as well as a fix for the double data entries problem noted earlier. Thank you for the original fix you gave for that bug.
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now you have it. That is basically what I had to do. It cannot be done in the time domain.
Yes it can. If you have a signal you measured in the time domain then just add the onefn data vector to it. If you have a signal that was measured in the frquency domain then obviously you will have to either transform the signal to the time domain or the onefn vector to the frequency domain before they can be added.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
Pictures are worth a thousand words. Attached are a couple of graphics files that should help. The first shows just the baseband signal I am working with and the second shows physical 1/f noise added to that baseband signal in the frequency domain done as I previously described it has to be done.
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is your baseband signal measured in the frequency domain or the time domain?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have it in both the time and the frequency domain. When I added the onefn to the time domain I ended up with the symmetry problem in the frequency domain.
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you take your time domain signal and CFFT it without adding any noise you will see the conjugate symmetry. If you take ANY real valued signal and CFFT it you will see the conjugate symmetry!
It's not a problem, just a property of CFFT. Just throw away the extra points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The time domain signal is complex. When I take the CFFT of it, I see what I sent in the second picture. There is no symmetry.
Bill





