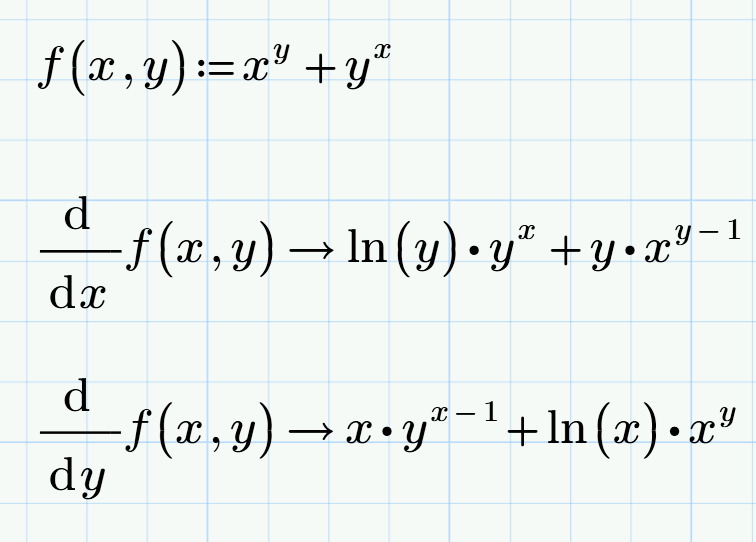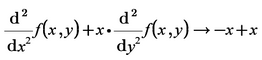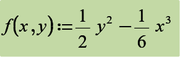Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Mathcad Prime 7 bookmaker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad Prime 7 bookmaker
In February 2021, we will receive Mathcad Prime 7.
I am betting $ 100 (8000 rubles) for the animation in the new version of the package.
I am betting $ 70 for the fact that the new version of the package will be able to show dll functions in the function window.
I am betting $ 50 for the fact that the new version of the package will be able to link to Mathcad files on the Internet.
What money would you like to put on what old and new opportunities?
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Somebody, please check on Valery, he's not thinking clearly!
And please don't take advantage of him and take his bets. 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
$20 linking inside workbooks
$10 table of contents
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, "Prime 6" is a contradiction. "Prime 7" is not. 😎
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1¢ their alarm clock will ring in February and they will wake up and see they've got nothing to show, so set it to 2022.
5¢ they will find a guy who made something at home out of boredom, and wants to sell them. That will be Prime 7.
10¢ someone will reverse-engineer the Creo-MC interface and make SMath work with Creo. That will be the end of Mathcad.
25¢ they will close the Mathcad department, sell it for a bottle of sangria, or make it Open Source.
50¢ they will forget about Mathcad, stop updating the information on the webpage, it will transition to the category of forgottenware (not to be confused with abandonware).
Ok, that's as much coins as I found in my drawer. Can get rid of them any other way as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1000$ - indexes in texts
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1$ somebody at PTC wil suggest to buy Excel because the graphing features are good enought for MC Prime. On failing that they will resort to Lotus 1-2-3.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Freecad has the spreadsheet with physical units. Quite useful!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery, what about the partial derivatives solver?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think we do not need an espesial view for this operator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's about finding the partial derivatives. How would you solve this PDE?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You wouldn't use Mathcad. You'd use Mathematica, Maple or Mupad. This is Maple (works in Mathematica as well):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is it possible to solve that [articular equation using the numol solver of Mathcad Prime?
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think numol is limited to eliptic or hyperbolic PDEs. The tricomi equation is mixed eliptic-hyperbolic, so perhaps yes, numol will solve it. Please try and let us know
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I couldn't find any way to solve the Tricomi equation by numol or any other PDE solver. Then I tried to do symbolically using
but I get only the trivial solution x=0, instead of the nontrivial
If anybody can suggest anything would be appreciated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
where is Mathcad Prime 7.0? It's already March (with hope).
When people wanting something hear "March," they think "March 1st!"
When people making a commitment say "March," they mean "March 31st!"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
😃