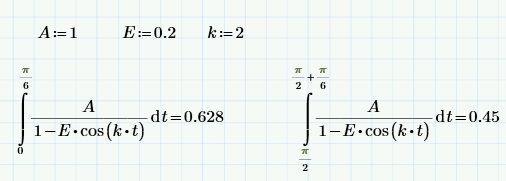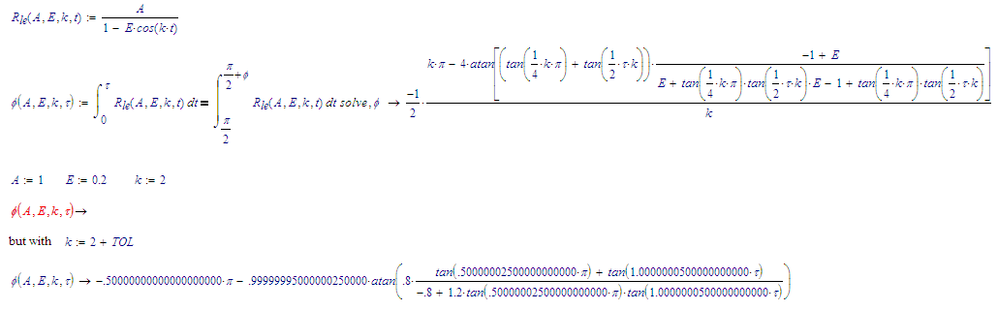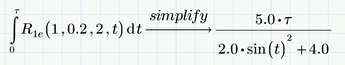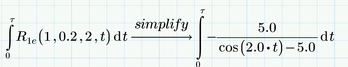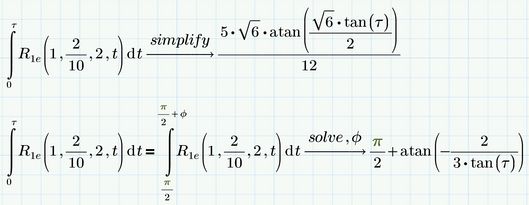I don't believe your second line
By one example
DON'T TRUST SYMBOLICS, they were never strong
In such cases, first solve symbolically, then apply the numbers. Now:
Notice how the result for phi(A,E,k,tau) will result in an error when I try to evaluate it with the given data. The reason is that in the solution for phi there is a tan(k*pi/4) occurring a few times. With k=2, that results in tan(k*pi/4)=tan(pi/2) which is undefined, or infinite, whichever you like better. This is the cause why your symbolic answer can produce an erratic answer.
If I change k a tiny bit different from 2, a valid result appears.
Success!
Luc
The problem occurs once again because of Primes outrageously auto labelling feature, which ever so often does not work as it should and makes more pain than blessings.
Look how Prime simplifies one of your definite integrals:
This is definitely wrong as the result should not contain any occurrence of variable t any more. The reason for that error is, that Prime label the "t" as argument in function R.1e as "variable", but the "t" in the differential "dt" as "automatic".
And as Primes symbolic, when trying to solve your equation, first simplifies the integrals, it comes to the wrong solution Phi = tau.
If you correct this error by labelling both "t" the same (either both as "variable" or both as "auto"), it looks like Prime can't give you a result for the integral
and consequently is also not able to solve your equation
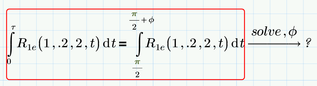
BUT .... the reason this time is that you used a floating point number (0.2) which unfortunately forces Primes symbolic to some sort of float mode. If you change 0.2 to 2/10 (or 1/5, of course), Mathcad is able to calculate the integral and is also able to solve your equation (after a while of "thinking").
The calculations below in your sheet are correct, as Primes auto-label feature worked correct here and all "t" are labelled the same.
