Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Matlab vs. MathCad and Solve Blocks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Matlab vs. MathCad and Solve Blocks
I am trying to translate some Matlab programs into MathCad. My question is highlighted below and the worksheet is attached. Thanks in advance for any help.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have to use the "Insert image" button to insert pictures in the context of a discussion. Just copy and paste doesn't work.
EDIT: Its not clear to me what you are trying to do at the end of your file, but minimize() can be used standalone without a solve block, too, if you don't have to provide any constraints. Not sure, though, if its really the function you need.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yep, that dawned on me. Here it is...

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You refer to the function fminbnd, but no such function exists in your worksheet. What is this function?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
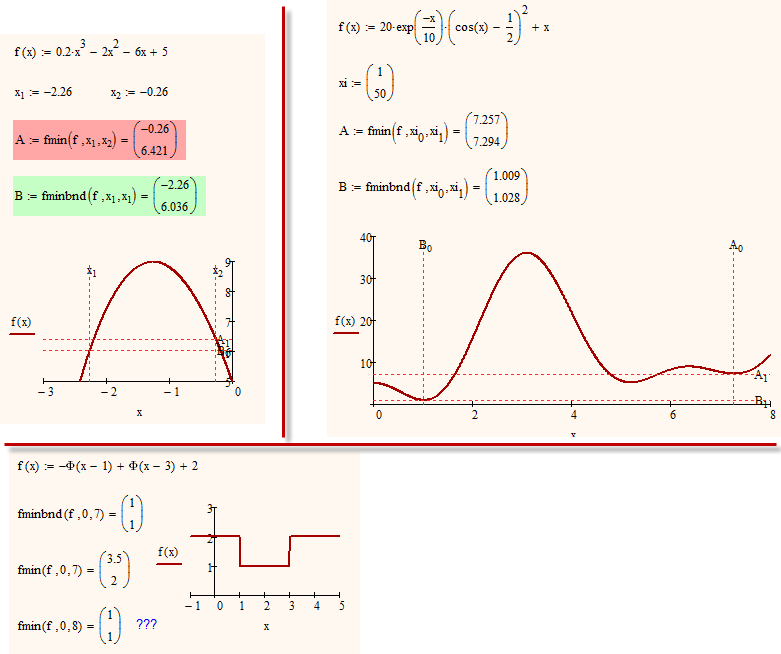
I guess I was not very clear. fminbnd is the Matlab function. fminbad (func, a, b) finds the minimum of func in the interval [a,b] (Note: funct depends on a single variable). I thought Minimize in MathCad was similar but had to be used with a solve block. Werner pointed out that it can be used alone, but now I see that it is for multi-variable functions. I guess I am looking for something like the MathCad function root, but for the minimum of a single variable function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Which function do you want to minimize and in what interval?
A multivariable function would work with a single variable function as well, but I fear you want to minimize a function with more than one argument, vary only one of them and hold the others constant.
I remember that minimize made troubles when used in a program and it also cannot be turned into a function (as if I guesss right would be necessary here). It will also not work with locally defined functions.
You may write a brute force fminbnd(func,a,b) yourself but it would lack of precison and probably be rather slow.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You probably need to define timeinterval as a separate function. If you upload the Matlab source code (it's just text) I'll have a look. It's not totally clear (to me) exactly what is required based on what you've provided so far.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My guess is that the next command determines the minimum of the function "distancefromrim" where v0 is v, theta is x*pi/180 and only t varies between the two values of timeinterval.
Mathcad doesn't offer an equivalent to minbnd() and for reasons beyound me we unfortunately can't turn a solve block with minimize() or the standalone minimize() into a function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
for reasons beyound me we unfortunately can't turn a solve block with minimize() or the standalone minimize() into a function.
I'm not sure why you think that to be the case.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Missed that reply of yours.
for reasons beyound me we unfortunately can't turn a solve block with minimize() or the standalone minimize() into a function.
I'm not sure why you think that to be the case.
Because I tend to forget that the objective function has to include allarguments of the function we wish to create even though its not using them (in our case the time limits).
I dawned to me after I wrote this and I posted the appropriate sheet - 4 minutes late 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If my guess above is correct here is a possible solution using a solve block with minimize() turned into a function (I always forget how to turn minimize in a function and am wondering why it doesn't work in first place but after a while it dawns). Be aware that minimize is in no way reliable (see my comments in the attached file).
BTW, does anybody know if it is possible to turn minimize() into a function and provide the function ti minimize itself as an argument?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If my guess above is correct here is a possible solution using a solve block with minimize() turned into a function (I always forget how to turn minimize in a function and am wondering why it doesn't work in first place but after a while it dawns). Be aware that minimize is in no way reliable (see my comments in the attached file).
The order of the arguments matters. Specifically, in the objective function the parameter that is to be varied to minimize the function must be the first argument. I have no ieda why. This is also true for maximize.
BTW, does anybody know if it is possible to turn minimize() into a function and provide the function ti minimize itself as an argument?
Yes. Here's a worksheet from Tom that shows the neat trick that is required to do that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks! I will give it a look.
In the meanwhile I have been working on a fminbnd() lookalike and how to use it with multiargument functions.
Its not tested but it seems to work. Its a brute force attack which refines its result recursively (at the time not until a certain precision is reached but just a certain numbver of times). The file also shows how to use it with multiargument functions. Also attach John's sheet to show how to use it in the context of his file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You say in the worksheet "Constraint is a soft one, so no guarantee that the solution returned is really inside the interval.". For minimize, maximize, and find, constraints are hard constraints. For minerr they are soft constraints.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the correction! I wasn't quite sure about that anyway, obviously got confused as of minerr.
Indeed the result will be in the interval provided, but it will not necessarily be the absolute minimum in that interval.
Cant think of anything but (more or less) brute force approach, like the routine I posted, to do the job.
We could look at the left and riight limits, root the first derivative, but again with numerics we will only get one solution, not all. Furthermore we would have to deal with discontinuities of the function itself or its derivative.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oops! ![]()
The center is not allways the best start value and as already written, minimize will give you one local min, but not necessarily the absolute min. I guess we could also find examples where minimize would find a local min but another local min is smaller.
EDIT: Found an example and integrated it in the pic above. 😉
You could try a couple of start values at small distance, but then we are at brute force again. ![]()
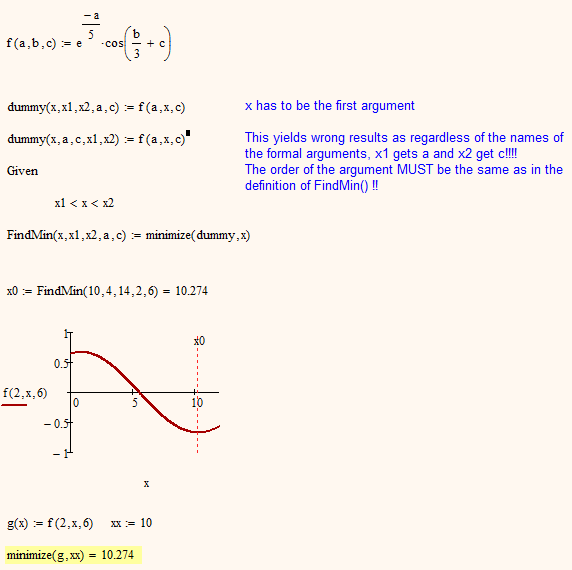
BTW, any special reson for that special definition of RApply? Wouldn't it be OK the way Tom has done?:

The order of the arguments when turning minimize into a function are a very strange thing. Its not only that the variable which should be varied has to be the first, also the order of the other arguments matters:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner and Richard: It will take me some study to digest this, but thanks for the help, interesting discussion, and education!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
The center is not allways the best start value and as already written, minimize will give you one local min, but not necessarily the absolute min. I guess we could also find examples where minimize would find a local min but another local min is smaller.
EDIT: Found an example and integrated it in the pic above. 😉
You could try a couple of start values at small distance, but then we are at brute force again.
Well, sure, the limitations of standard minimization routines are well known. Implementing a multistart version would be easy, and would find the global minima in your examples. And a multistart version of an efficient minimization algorithm is not what I would call "brute force". Your algorithm assumes that the global minimum is not so narrow compared to the range of the function to be searched that 10^4 steps will not miss it. There's no guarantee of that though. In fact, because you do not search within each of your steps, it's possible you could pick the wrong increment to pass to the next recursive call (imagine the global minimum is in increment 1, but the start of increment 1 happens to be larger than the start of increment 2. Then, unless I misread what you are doing, increment 2 will be passed to the next call in the recursion).
BTW, any special reson for that special definition of RApply? Wouldn't it be OK the way Tom has done?:
At one point I couldn't get it to work any other way. Then at a later point I couldn't get it to work anyway, unless I changed the order of the arguments. It seems that doing so also fixed the earlier problem, so you can actually just have f(x) on the RHS.
The order of the arguments when turning minimize into a function are a very strange thing. Its not only that the variable which should be varied has to be the first, also the order of the other arguments matters:
That is for sure. Is seems that in the case of RApply the first argument must be x, the second argument must be f (that's what I changed to fix the problems noted above). The other arguments can be in any order, but the order must match the order in the function definition that terminates the solve block. It's as though they are being passed by order, rather than by name.
BTW, are you going to post a worksheet with your "nasty" cases in it, or are you hoping I will retype everything ?![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And a multistart version of an efficient minimization algorithm is not what I would call "brute force".
OK, that kind of algorithm sure would be much more sophisticated than the steamroller tactics in my routine, but still it would have something of a brute force approach. There never will be a 100% algorithm as long as we are using a numericial approach. I guess we could find examples which fail even if I would use your fmin on every of my 10^4 intervals.
(imagine the global minimum is in increment 1, but the start of increment 1 happens to be larger than the start of increment 2. Then, unless I misread what you are doing, increment 2 will be passed to the next call in the recursion).
No, if the start of incerement 2 happens to be the minimum of all 10^4 samples, the next search takes place in increment 1 AND increment 2, one step to the left an the right of the current minimum. The min() and max() shall only ensure that we do not fall out of the interval. But of course it would be easy to find examples where this "algorithm" fails to find the gloabal minimum - a thin spike or a very high frequency signal should do. Using your minimization fmin on every interval (we wouldn't need 10^4 and no recursion would be needed) - basically thats what you call multistart, I guess - wouldn't be bullet proof but probably as near as we can come with reasonable costs.
The other arguments can be in any order, but the order must match the order in the function definition that terminates the solve block. It's as though they are being passed by order, rather than by name.
Anyway, its mystic to me. Especially dangereous, as a wrong order of arguments sometimes doesn't let the routine fail but simply return a wrong result.
I guess all those tricks will not work in Prime. At least a standard trick like
f(a,b):=a*sin(b)
g:=f(2)
and that way defining like g(x):=2*sin(x)
doesn't work anymore.
BTW, are you going to post a worksheet with your "nasty" cases in it, or are you hoping I will retype everything ?
I did not think it would be of such great interest - here it is 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's the multistart version. If there are multiple equivalent minima, I made it return all of them.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Great, thanks! Sure something for the toolbox.
Any chance of getting rid of the duplicates (the true ones and the approximate like in the pic) other than decreasing the value of TOL?

Increasing the number of intervals makes the effect worse of course and we would have to decrease TOL down to 10^-8 to cope with that effect.

BTW, the example is from the last function in the file you posted.
I guess it would be necessary to write ones own match routine as normal comparison operators are not affected by TOL.
I have no example for "exact" duplicates, but they may occur if the minimum is exactly at the beginning/end of an interval.
EDIT:
Here some other nasty effects and decreasing TOL doesn't help in those cases

OK; the first one is neither nasty nor a problem. If I provide just 10 start values I can't expect 11 different results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I fixed the near duplicate and true duplicate problems (which was quite a lot of work!).
For the other issues: 5 is missed when N is 10. Sure. If you have many minima and not many increments for the multistart, it can miss minima.
The accuracy issue: If you show more decimal places you will see it elswhere too. It's dictated by the convergenge of minimize. It should be possible to improve this by chnaging the value of TOL above the solve block, but it doesn't seem to work. A bug, I guess, so there's nothing I can do about it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well done!
I was working on my own version and attach what I came up with. Its slower than yours (no wonder, I call fmin for every value returned at least three times).
Accuracy concerning finding the global y-min is sometimes slightly better, but in the last example your routine definitely yields more exact x-values than mine.
In one case at the end your routine still misses a duplicate
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
WE and A.Non - thanks again! Works like a charm. In my app, I do not expect to encounter the many special cases you have treated, but comforting to know they could be.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So you already are able to improve you Basketball Free Throws skills?
How about sharing the final sheet?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
So you already are able to improve you Basketball Free Throws skills?
How about sharing the final sheet?
I am afraid whatever skills I had have so deteriorated with age that I am reduced to theoretical analyses. Would be happy to post the worksheet if I ever finish it but at the moment I am having a problem using Maximize as a function. I thought I was following the example you gave but I am probably doing something stupid.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As was discussed above, turning minimize or maximize into a function can be very tricky and the order of arguments matters. You must reverse the order of the arguments in the definition making it "distancefromback(theta,v):=...
.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In one case at the end your routine still misses a duplicate
Good catch. Actually a symptom of a serious logic flaw. I think the new version works properly though.






