Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Matrix inverse Error
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Matrix inverse Error
Hi
I am unable to calculate inverse of the matrix. The result is taking accuracy upto 3 decimal places. Even I tried to change decimal precision from "Math Formatting Option but the error become unchanged. "Please find given image and attached file for your reference.
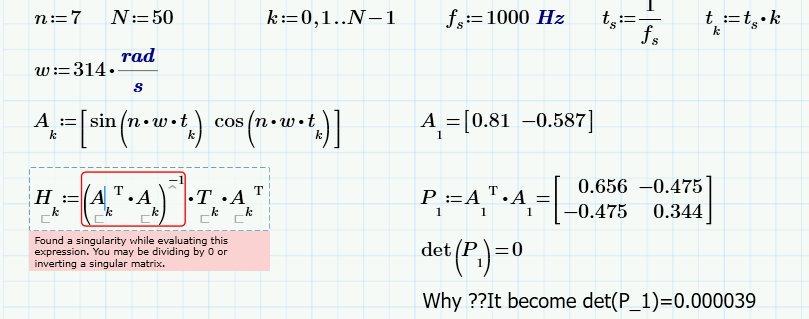 for your reference:
for your reference:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not sure what you mean by your final comment, or where 0.000039 comes from. The determinant of your matrix is zero. Always.

Edit. I figured out where you got 0.000039 from. That's what you get if you copy and paste the result matrix, with three decimal places, and then take the determinant. So it's non-zero because of serious round-off error. Changing the precision under math Formatting has no effect on the precision of the calculations, only on the precision of the displayed result, and will not generate that result.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As Richard had shown, any matrix which is built the way you build yours by multiplying any column vector with its transposed pendent gives you a matrix with a zero determinant and so ins not invertible.
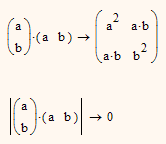
You calculated with the values you see

but Mathcad calculates with much more precision. So what you experience when you get 0.000039 is just an approximation of the real result, at best valid up to three decimals (you can't expect the result with a better precision than the input values) . And if you round your result to three decimals, you get .... Bingo!
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your response but in my application the number 0.000039 has its own significance. Please let me know if we can get this result by any means. Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Perhaps if you told us what the significance of 0.000039 is we might be able to suggest a way to get the result you want. Without that information it's not possible to suggest anything.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But the matrix you create will have a determinant of zero for any value of omega, n and t.k.
The value 0.000039 ist just an approximation for zero due to the fact that you just use values rounded to three decimals!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Additional remark:
If you want Mathcad to calculate with inexact, rounded values, you would have to tell Mathcad so. Then you get the, for some reason significant, inexact and rounded value 0.000039.
Maybe this clarifies the situation (you have not shown the value of n but it looks like its 6.995):

The screenshot is of Mathcad 15, but it should be the same in Prime. You will have to change the display precision to more decimals to see the ....10^-17 value. If you leave it at the default (3 decimals), you will see 0. The same applies to the value 0.000039 at the end.
You already introduced an inaccuracy when you defined omega. Mathcad provides the unit "Hza" for this purpose or you may use the predefined constant pi to calculate with.
BTW, in which way would an inexact, rounded value be significant ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
BTW, in which way would an inexact, rounded value be significant ?
Because it's the answer in the hand- / sliderule- derived (to 3 digits) textbook/lecturer's notes answer? ![]()
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> Because it's the answer in the hand- / sliderule- derived (to 3 digits) textbook/lecturer's notes answer?
Guess you are right. This would just explain why Sameer expected that result, but not why "the number 0.000039 has its own significance" ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guess you are right. This would just explain why Sameer expected that result, but not why "the number 0.000039 has its own significance"
It is the duration, in ms, of the nuclear reaction when the largest nuclear bomb (the Tsar bomb) was exploded. ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And I thought its because of

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Richard Jackson wrote:
Guess you are right. This would just explain why Sameer expected that result, but not why "the number 0.000039 has its own significance"
It is the duration, in ms, of the nuclear reaction when the largest nuclear bomb (the Tsar bomb) was exploded.
And I thought its because of
![]()
... or even
or 1 microstep ... (probably would only make sense to a Brit ![]() )
)
Stuart





