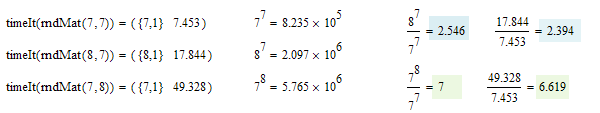- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Matrix path
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Matrix path
I am trying to work out how to calculate all the paths from each cell in column zero to the end column.
This is part of project to calculate the remaining strength in a material. The matrix represents a grid on the material. Each cell in the matrix contains a measured parameter at a location on the grid.
I need to calculate the sum of all the paths available from each of the cells in column zero. The path can progress one cell up or one cell down or one cell across. It can never go backwards.
In the attached file is a grid of 5 x 7, with fictitious data. In reality the grids are more likely to be 20 x 40.
I can see how to do it manually but I cannot see how to do it within Mathcad.
Any direction or guidance would be appreciated.
The system will not allow me to attach a file. "The contents of the attachment doesn't match its file type", which is nonsense because it is an mcdx file.
Thank you
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
please explain how do you calculate the sum of all the paths manually.
Martin Hanák
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good Morning Martin,
Thank you for replying to my post.
I mapped out the first few rows manually. For example, if we assume an origin of 1 and the rows labelled A to D and the columns 1 to 7 and we start at cell A1.
A1 can go to A2 or B1. If it goes to A2 then it can go to A3 or B2. If it goes to A3 then it can go to A4 or B3 etc.
A2 can go to A1 A3 and B2 etc.
From that you can build up all of the paths possible from A1. Then you have to move to A2 and repeat the performance.
Then you can sum up the value total for each path and perform various calculations on them.
I hope that is clear.
Kind Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are still some questions.
1) Is the following correct: We never go to the left and we never go back (up or down) from where we came. That way endless paths are excluded
2) Where does a path end. You wrote that it spans from the first column to the last one.
2a) Are we allowed to go up or down when we reach the rightmost column or
2b) do we have to stop immediately when we reach the first time a cell in the last column?
In other words: Is C1-C2-C3-B3-B4-B5-B6-B7-C7 a valid path or not?
3) What should the result be? You wrote "I need to calculate the sum of all the paths available from each of the cells in column zero." What means "sum of all the paths"?
3a) Are you just interested in the number of paths possible from each of the cells in the first column. The result being a 5-element vector representing the number of paths for each of the 5 start cells.
This is probably not what you are looking for, as the values in the cells would be irrelevant and the result would be the same for any cell in the first column -> r^(c-1) if you have a r x c matrix.
3b) Do you intend to add all numbers for all paths possible from a start cell? The result being a 5-element vector and each element is the total sum of of all cell values for all paths possible from each of the 5 start cells.
3c) Similar as 3b), but this time the sum of values is listed separately for each path. That way for each start cell we would have a list of results. The result could be either represented by a nested 5-element vector and this time the elements would be vectors again, representing the cell sums of each of the 15625 paths possible from a start cell. Or you could represent the result in a 5 * 15625 matrix.
You will of course loose any information as to which path which value belongs to.
For a 20 x 40 matrix the result would be a matrix with 20 rows and 5.498*10^50 columns!! Guess this is also not what you are looking for, right?
Whatever the result should be - I think that the easiest approach would be a function which is called recursively. There is no easy, ready-made function available you could use out of the box. You will have to use some programming.
I can't read your file with my version of Prime so I can't see if you just provided a 5 x 7 matrix or if you already have tried some approach. You may consider attaching a screenshot or a pdf-print of your file in the latter case.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, I gave it a try.
I am assuming that from my reply above that 1) , 2b) and 3b) apply.
Its just a quick hack and it seems that it will be almost endless until a calculation for a 20 x 40 matrix finishes.
A recursive appoach often is the easiest one, but seldom the most efficient or most reliable one.
So while my program sure can be improved I guess for a substantial better performance you would have to chose a different approach.
I attach the file in Mathcad 15 format and provide a screenshot. You may either convert the file or retype the small programm if you want to give it a try.
If you look at the formula for the number of possible paths I sent in my previous post, its no surprise that adding rows rather moderately increase the calc time but adding columns let the time explode. After all the rows are at the base, but the columns in the exponent (n = r^(c-1))
Based on those numbers a 20 x 40 matrix would take about 3 * 10^39 years. Even if your machine is 100 times faster than mine ..... you sure won't want to wait.
Guess a better approach than the brute force recursive one may be to find a formula to determine how often a cell is part of a path.
EDIT: Just realized that my program seems to return wrong results!!
Have to recheck if I have some more time.
In the meantime waitung for your answers to all the questions above.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
Thank you. I will copy the program into Prime and run it.
Kind Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@klax wrote:
Dear Werner,
Thank you. I will copy the program into Prime and run it.
Kind Regards
No! Don't do that! Read my comments about calculation time and look at my EDIT. The program returns wrong values (I missed a few cells in recursion).
Rather answer the questions above to make sure, what you really need!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is the corrected routine.
Still the same issue with calculation time, of course.
Still waiting for your answers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
Thanl you for your continued interest.
Here are the responses (I have coloured themblue to make them easier to pick out):
1) Is the following correct: We never go to the left and we never go back (up or down) from where we came. That way endless paths are excluded Correct. Note that diagonal moves are not permitted in any direction
2) Where does a path end. You wrote that it spans from the first column to the last one. Path ends at the last column
2a) Are we allowed to go up or down when we reach the rightmost column or. No.
2b) do we have to stop immediately when we reach the first time a cell in the last column?
In other words: Is C1-C2-C3-B3-B4-B5-B6-B7-C7 a valid path or not? Not valid. You can only go one cell at a time, so from C1 you can only go to B1 or D1
3) What should the result be? You wrote "I need to calculate the sum of all the paths available from each of the cells in column zero." What means "sum of all the paths"? Each cell has the data relating to the material condition at that point. The sum of the material loss at each location on the path is averaged and then applied to a formula which gives the remaining strength. This calculation is applied for all paths.
3a) Are you just interested in the number of paths possible from each of the cells in the first column. The result being a 5-element vector representing the number of paths for each of the 5 start cells.
This is probably not what you are looking for, as the values in the cells would be irrelevant and the result would be the same for any cell in the first column -> r^(c-1) if you have a r x c matrix. It is not just the number of paths but the actual route of each of the paths that is important.
3b) Do you intend to add all numbers for all paths possible from a start cell? The result being a 5-element vector and each element is the total sum of of all cell values for all paths possible from each of the 5 start cells. Yes
3c) Similar as 3b), but this time the sum of values is listed separately for each path. That way for each start cell we would have a list of results. The result could be either represented by a nested 5-element vector and this time the elements would be vectors again, representing the cell sums of each of the 15625 paths possible from a start cell. Or you could represent the result in a 5 * 15625 matrix.
You will of course loose any information as to which path which value belongs to.
For a 20 x 40 matrix the result would be a matrix with 20 rows and 5.498*10^50 columns!! Guess this is also not what you are looking for, right? Right!
Whatever the result should be - I think that the easiest approach would be a function which is called recursively. There is no easy, ready-made function available you could use out of the box. You will have to use some programming.
I can't read your file with my version of Prime so I can't see if you just provided a 5 x 7 matrix or if you already have tried some approach. You may consider attaching a screenshot or a pdf-print of your file in the latter case. I just provided a 5 x 7 matrix with some random values in.
Kind Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
2b) do we have to stop immediately when we reach the first time a cell in the last column?
In other words: Is C1-C2-C3-B3-B4-B5-B6-B7-C7 a valid path or not? Not valid. You can only go one cell at a time, so from C1 you can only go to B1 or D1
???? I am confused now. A, B, C etc. are the row headers and going from C1 to C2 would be a step directly to the right. Which from what you wrote so far should be valid. After all you wrote yourself that a step from A1 to A2 is valid!!??
The question was meant to clarify if it would be valid to go down one step from B7 to C7 in the last column and as I suspected thats not a valid move as the path stops at B7 (given a 7-column matrix).
3) What should the result be? You wrote "I need to calculate the sum of all the paths available from each of the cells in column zero." What means "sum of all the paths"? Each cell has the data relating to the material condition at that point. The sum of the material loss at each location on the path is averaged and then applied to a formula which gives the remaining strength. This calculation is applied for all paths.
And the values of all the paths possible from one cell in the first column are added, too, as I understand.
So it looks the guesses I made were correct and the last file I sent does what you demand, right? (Apart from the confusion in point 2b) which has to be clarified.
As I understood so far you can go from every cell either up, down or to the right, but not back to from where ypu came (if it was from above or below). So a step to the right from C1 to C2 should be allowed!? Or do I miss something.
The routine I provided follows every possible path and given a 20 x 40 matrix this means it would have to follow 20^39 different paths which takes too long to calculate - it won't finish in a lifetime.
I haven't found a suitable iterative algorithm yet. I just developed a routine which creates matrices for every cell in the first row where every cell would indicate how many paths a cell is involved to. Using this matrices its very easy to quickly calculate the desired values.
Unfortunately my way of obtaining those matrices involve the very same recursive algorithm and so there is no benefit.
If you find a quicker way to determine how many paths use a specific cell you would have found a quicker way to get the values you are looking for (simple vectorized matrix multiplication).
Can you confirm that my routine, lets say for the 3x3 matrix with the numbers 1 to 9, creates the values you are looking for. Or can you provide the values for that very matrix you expect as result?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Looks like I found a way to cut down calculation times.
A 20 x 40 matrix takes now less than half a second (quite a difference to 10^39 years)
I am still not fully satisfied but I guess thats something you could use. I have the feeling that I don't see the easy way to determine the values in those three columns (you'll see what I am talking about when you look in the files).
I am attaching the MC15 file, a pdf print and a converted file in Prime30 format.
Converting to Prime reminded me to why I hate Prime and don't want it to use. Editing is so cumbersome and Prime refused the recursive local function and insisted it has to be a global one 😞
So I had to define those functions on worksheet level.
You may also notice that calculation time nearly doubles in Prime.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
I am studying the program that you kindly sent. Your knowledge of programming and matrices is obviously light years ahead of mine so I will have to work through it slowly to understand it!
Thank you for your continued interest, I will get back to you as soon as possible.
Kind Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
You are correct. It is possible to go from C1 to C2 to C3.
Kind Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
1.]
If I understand you well, the path can start in any matrix cell. This means in 1,1 an also in 3,7 (for example).
2.]
If I understand you well, the path ends in 7th column. This means step from 2,7 to 3,7 is forbidden.
3.]
Are you able to create program solving your problem in any programming language ? I mean Basic, C, Pascal, ...
Martin Hanák
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
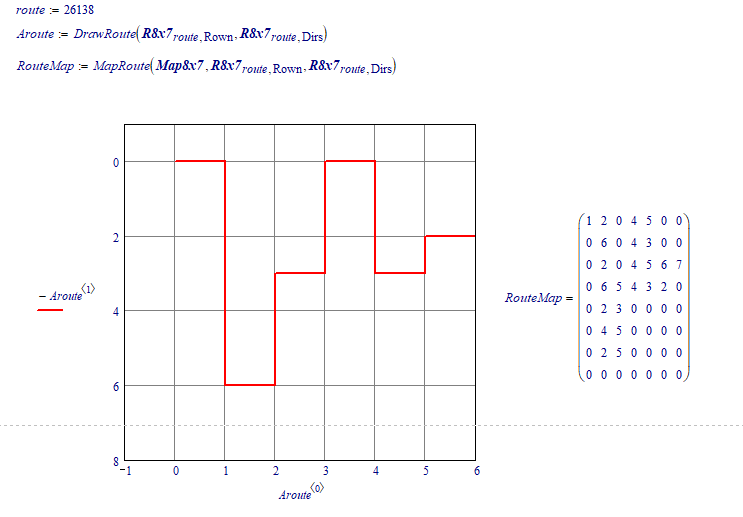
It appears to me you want to have the path for each route as well.
I made one simplification: starting in the first column, a route can only go left as the first step.
Here is the implementation and some results.
Of course, with the amount of informatioin stored, the maximum array size determines the maximum size of the original matrix that can be processed successfully.
It appears that in Mathcad 11 8x7 is the largest size.
Maybe Prime allows to go further, but (as Werner already observed) there's also a (calculation) time aspect. Time grows exponentially with matrix size.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just a thought...
Would it not be more realistic if the crack direction was (at least partly) chosen by data in the matrix?
I could imagine that a crack route has a preference for the surrounding cell with the smallest (or else the largest) value of the three (up, forward, down) cells. But I have to admit that I have no idea about the actual meaning of the matrix cell values...
But if this knowledge could be used, then a single route would result from each of the starting points, which would not only make the result matrix much shorter, but it would also calculate faster because less paths have to be investigated by the recursive routine.
Luc