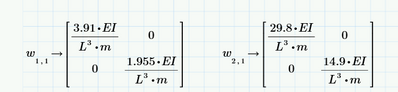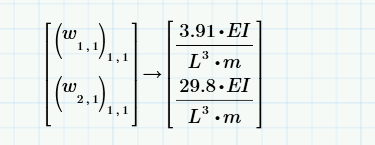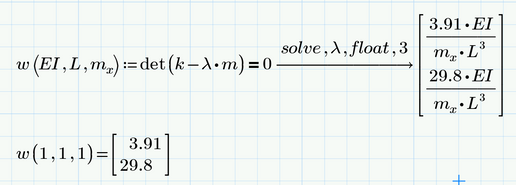Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Matrix terms are reversed when evaluated symbolically
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Matrix terms are reversed when evaluated symbolically
when evaluating frequency equation for a MDOF model, if the stiffness and mass matrices are defined in terms of mass, elasticity, and etc constants, the resulting terms of the symbolic evaluation are reversed. (see below). I know that the result in terms of the constants is the correct answer. However, I dont understand why the determinant using values only gives reversed terms? Any ideas or pointers are apprieciated.
Thanks
Solved! Go to Solution.
- Labels:
-
Civil_Engineering
-
Mathcad Usage
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I see no problem here.
There is no rule or convention about the order in a set of multiple solutions to an equation.
Its quite possible that the symbolics returns the solutions in a different order depending on if just numbers are used or variables & units.
As we don't know how the symbolic "solve" is implemented internally we can't say why.
WHY IS MATHCAD GIVING ME a DIFFERNT result than expected?
Mathcad gives you a correct result - it can't know what you expect 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's a follow up.
correction: Im not sure which is the correct answer. when solving the equation by hand the roots are as follows
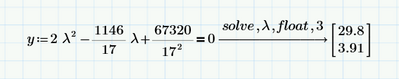
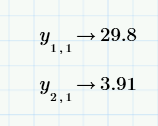
WHY IS MATHCAD GIVING ME a DIFFERNT result than expected?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I see no problem here.
There is no rule or convention about the order in a set of multiple solutions to an equation.
Its quite possible that the symbolics returns the solutions in a different order depending on if just numbers are used or variables & units.
As we don't know how the symbolic "solve" is implemented internally we can't say why.
WHY IS MATHCAD GIVING ME a DIFFERNT result than expected?
Mathcad gives you a correct result - it can't know what you expect 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
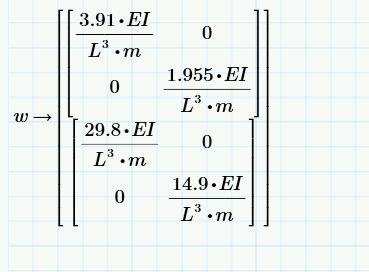
Thanks Wener_E! it seems logical. It was my initial thought, but what about the embedded matrices? I cant make sense of those extra terms?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@MI_10648350 wrote:
Thanks Wener_E! it seems logical. It was my initial thought, but what about the embedded matrices? I cant make sense of those extra terms?
Which extra terms?
Do you talk about the nested matrices when you evaluated the variable "w"?
You don't show how "w" was calculated, so I can't say anything about it.
BTW, apart from showing pictures you sure should attach the worksheet itself.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is the worksheet. However, for some reason the nested matrices disappeared! not sure what happened, but its the same exact code I wrote earlier. Im still new to symbolic evals so I guess I have a lot to learn.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hard to say what cold have caused Prime to give you the nested matrices for "w".
Chances are that you had defined something differently from whats now in the sheet or that you deleted some definition you had.
It looks like you use a n older version of Prime (P6 or below) which uses the older symbolic muPad (which was in many respects more capable than the new one, an Axiom fork).
Here is what I see in Prime 9 when I recalculate the sheet.
As you can see its necessary to use "assume,ALL>0" to get a similar result as you got with muPad.
Actually the new symbolic is correct because sqrt(x^2)=x is only valid if x>=0. Generally sqrt(x^2)=|x|
BTW, you can always assign the result of the symbolic evaluation to a function instead of a variable and so can get the numeric results in the same order as the symbolic results:
And o fcourse because you use Mathcad/Prime you should take advantage of its strength and use units throughout.