Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Memory problems stacking Matrices
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Memory problems stacking Matrices
I have a small programm trying to split a matrix depending on the content in the rows. Now I'm using the folling algorithm:
take the row as submatrix on the actual position
stack that on one of the two alternative matrizes depending on a condition
Unfortunately this has a very poor performance both time and memory wise.
Assigning the rows via i,j to a new matrix seems to be better. Any ideas why?
thanks
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You didn't include the faster routine without using stack. But you are right, without stack the routine is MUCH faster! I don't know why - you would expect built-in routines to be more efficient than self written loops.
In the attached sheet you find 8 different split-routines. I have no idea how I could judge memory consumption other than watching process mathcad.exe in task manager which would be very unreliable, to say the least. So I have concentrated on time taking. In the pic you see the calculation times needed for splitting 10 times a 1000x1000 matrix.
The splitting routines:
split0: is your original program
split1: damp sqib; here I tried to replace the row selection from submatrix to a transpose/column/transpose combination and the routine went a lot slower (factor 10!). Transposing the whole matrix for every row obviously does cost a lot of time
split2: went back to submatrix but included some improvements (getting rid of if/oherwises, unnecessary submatrix,..) Does not do much better and in the last runs I could not duplicate the double speed of this rotine which I mentioned in the file.
split3: transpose the matrix and work column-wise instead of row-wise. That way we can use the column selector. Very slight improvement of calculation time
split4: The lonely winner! Unfortunately we are cheating here, as this routine does return nested vectors. To access a single number you would have to type M[ispace[0,j instead of M[i,j. So it does not count
split5: Trying to use split4 but "flattening" the result to get the desired matrix. flattening uses stack, so again big slow down.
split7: Using method of split4 and a flattening routine which replaces stack by for loops. More or less ex aequo with split6
split6: usually number one in time ranking (not counting split4). stack, augment, submatrix replaced by for loops. As you wrote this is much quicker (factor 10 to 12) - strange.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please, post a worksheet!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ok here you are, data makes no sense- the programm collects all rows which have 0 in columns 0 and 1.
regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You didn't include the faster routine without using stack. But you are right, without stack the routine is MUCH faster! I don't know why - you would expect built-in routines to be more efficient than self written loops.
In the attached sheet you find 8 different split-routines. I have no idea how I could judge memory consumption other than watching process mathcad.exe in task manager which would be very unreliable, to say the least. So I have concentrated on time taking. In the pic you see the calculation times needed for splitting 10 times a 1000x1000 matrix.
The splitting routines:
split0: is your original program
split1: damp sqib; here I tried to replace the row selection from submatrix to a transpose/column/transpose combination and the routine went a lot slower (factor 10!). Transposing the whole matrix for every row obviously does cost a lot of time
split2: went back to submatrix but included some improvements (getting rid of if/oherwises, unnecessary submatrix,..) Does not do much better and in the last runs I could not duplicate the double speed of this rotine which I mentioned in the file.
split3: transpose the matrix and work column-wise instead of row-wise. That way we can use the column selector. Very slight improvement of calculation time
split4: The lonely winner! Unfortunately we are cheating here, as this routine does return nested vectors. To access a single number you would have to type M[ispace[0,j instead of M[i,j. So it does not count
split5: Trying to use split4 but "flattening" the result to get the desired matrix. flattening uses stack, so again big slow down.
split7: Using method of split4 and a flattening routine which replaces stack by for loops. More or less ex aequo with split6
split6: usually number one in time ranking (not counting split4). stack, augment, submatrix replaced by for loops. As you wrote this is much quicker (factor 10 to 12) - strange.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Wow you did a great job thank you so much.
I'm sorry the alternative looping solution was done for a similar problem where I found out that stacking is costly. You did the proof for this problem too. Great!!!
Let's see what PCT thinks about that 😉 Because of the impractibality to use Mathcad for real world simulation problems I now have an i7 CPU - and I will be testing Mathcad PRIME because it uses more than one core for the calculations, before switching to python back again....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
and here are the results when allowing Mathcad to optimize the programs
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Efried schrieb:
and here are the results when allowing Mathcad to optimize the programs
Just tried it myself and interestingly enough only split6 has profited by optimization by about 20-25%.
The other routines are not affected or even a little bit slower.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Efried schrieb:
Wow you did a great job thank you so much.
I'm sorry the alternative looping solution was done for a similar problem where I found out that stacking is costly. You did the proof for this problem too. Great!!!
I really wouldnt have expected that the built in routines stack and augment are performing that bad compared to self written loops.
Let's see what PCT thinks about that 😉
Wouldn't expect too much, but am open for a pleasant surprise, though.
Because of the impractibality to use Mathcad for real world simulation problems I now have an i7 CPU - and I will be testing Mathcad PRIME because it uses more than one core for the calculations, before switching to python back again....
Choosing the right tools for the task is not easy in every case. While a lot of people are using Mathcad in business for their "real world problems" with success, there sure are problems for which Mathcad simply isn't the appropriate tool.
I have just converted the sheet and the results of Prime are somewhat daunting. See below the comparison of two runs 1000x100 matrix 10 times, one with Prime, the other with MC15 on the same machine (slow, single core) . While I guess that the timing with time is not correct in Prime because of Primes attempts to simultanously evaluate regions, it took a lot more time in Prime2 to finish all calculations.
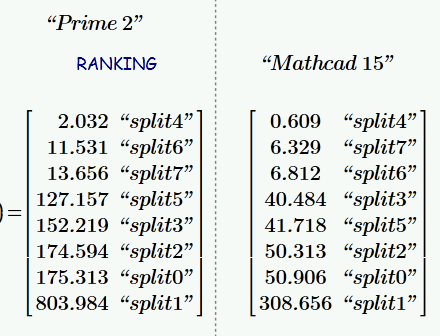
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
you are doing my job.
Ok so no Mathcad Prime for number crunching 😉
best
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok so no Mathcad Prime for number crunching 😉
Thats what it looks like. Maybe you should give it a try with a quadcore.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
yes a good idea - so far I do have a testing installation on the i7 dual core but should try to test it also on the i7 eight core machine. What was the easiest way to transfer the code from Mathcad 15 to Prime 2.0?
many thanks
best
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Efried wrote:
...What was the easiest way to transfer the code from Mathcad 15 to Prime 2.0?...
By using "Mathcad Prime 2.0 XMCD, MCD Converter":
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Vladimir, thanks a lot I have now tried this with my main weak document and it failed. After clicking on "include referenced documents" it hangs. Any ideas how to converts includes as necessary without crashes?
thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Efried schrieb:
Hello,
yes a good idea - so far I do have a testing installation on the i7 dual core but should try to test it also on the i7 eight core machine. What was the easiest way to transfer the code from Mathcad 15 to Prime 2.0?
many thanks
best
I should have mentioned that my testing was not only made with a single core but also with the 32bit version only under Win XP. So, while the results were disappointing, you possibly can make Prime2 perform better using it in a more modern soft- and hardware environment. Let us know about your results.
Conversion from Mathcad 15 to Prime2 format, has to be done using the "Mathcad Prime 2.0 XMCD, MCD Converter". This is installed with Prime2 but you have to have the lastest Mathcad 15 installed, too, to make it work (thats PTC logic, I guess). The converter can be used as stand alone program, as Valery has already shown, or from within Prime2 (ribbon "Ein-Ausgabe"). You should be aware that there is no way back - you cannot convert from Prime to "real Mathcad" format.
Find attached or your convenience my converted sheet which I had used for my test.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner, thanks so much. Here are the results of the trials using two cores...
for the eight I have to install the test version on my work horse.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
and here the result from the i7 run inserted into the picture of the i5 results

much faster!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Efried schrieb:
and here the result from the i7 run inserted into the picture of the i5 results
much faster!
Yes, but that does not necessarily mean that Prime would not be beaten by MC15 on that machine, too.
BTW, lets get rid of split1 😉
I am not sure if that timing makes any sense in Prime as it assumes a serial execution of every region one after the other.
Probably to get reliable results it could be necessary to test every routine in a single run.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thhe Mathcad 15 results where already posted above as pdf- here is a screenshot:
My only explanation from my C++ experience is that there might be a lot of sequential or even recursive calls for subroutines - which is the worst you can do, so stacking (version 0 ) is much slower in Prime but surprise the transposing trick in variant 1 is much better. Ther variants I would use namely 6 iand 7 is not significantly different...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Efried schrieb:
thhe Mathcad 15 results where already posted above as pdf- here is a screenshot:
I see. Wasn't sure which values came from which machine. So Prime is doing approx. as well on an i7 as MC15 on your i5? Shame on you, PTC!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
hello, no the Mathcad 15 versions are with the i7, I do not have a license on the i5 laptop.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Efried schrieb:
hello, no the Mathcad 15 versions are with the i7, I do not have a license on the i5 laptop.
OK, so at least on the i7 Prime live up (but not better) than Mathcad 15. So the ability to use the other cores and to calculate regions simultaneously seem to compensate for what the programmers have made worse in the relunch, compared to 15. Not a glorious chapter for PTC, either.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner, to be honest I did not understand your precautions with regards to the measuring technique. To be sure we have to know more about the internals. I guess the automatic calculation reuses some results if possible- also optimisation does it even more?
What is now the right way to perform the test?
thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner, to be honest I did not understand your precautions with regards to the measuring technique. To be sure we have to know more about the internals. I guess the automatic calculation
Yau are perfectly right in as much as we do not know enough about the optimization processes taken place.
The articel you referred to describes the situation pretty well.
My concern regarding the time measuring technique used are:
Lets assume we have a sheet with only two independend functions to evaluate (like the eval of the different splix routines) and every single of them would take one hour to calculate. In those functions I take the time at the begin, let the program do it work, take the time at the end and return the difference. In Mathcad 15 this would give me the pure calculation time with a very small overhead to consider and both routines would return a time of 1 hour each.
In Prime with multi-threading active (can it be turned off??) on a singleprocesseor/single core system the optimization of P2 would realize the the two functions are independent und would try to evluate them simultaneously. It would start both routines and switch back and forth between them. So both routines would get nearly the same start time and as both take about the same time to end theit calculations they will get approx. the same endtime, too. So both would report that it took 2 hours to finish their calculations (in reality they will even report more because of the overhead the task switching takes).
The same sheet on a multicore/multiprocessor system would run much quicker and as long as every thread has its own cor/processor for its own the time taken could be somewhat acurate, but usually Mathcad will create more threads than processors and so the time reported will not be useful. So the main problem with timekeeping is not th emulti-processor ability of Prime but the multi-threading with its pseudo-parallelization.
As long as we are not able to swtch off multithreading, I guess the best we can do is to evaluate every function singly (disabling the others or only recalculate a single one using F9).
This said I probably shouldn't blame PTC too much for the seemingly bad performance of my sheet under Prime in a single processor environment. The times reported can't be relied on.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
may be we can profit from that blog:
http://blogs.ptc.com/2012/05/16/multi-threading-multi-core-and-parallel-calculation-in-mathcad/
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oops, I just noticed that you can turn on/off multithreading and the switch is ecactly where you would think it should be 😉
I don't like to use Prime because of its slow reaction, the slow workflow as of the need to use the menues s o much, etc., so I have not the experience.
I tested it on my single core machine and found out that with multicast switched on Prime seems to try "parallel" processing at first but very quickly goes back to sequential operation. By this I mean that at the beginning I see 3 to four of these yellow "please wait I'm thinking" disks but soon it switches back to one after the other. So there is not much difference in time between the two modes.
What this means is that I was wrong in writing that we should not blame PTC/Prime for being so slow as it may be wrong results from the timing routine as an effect of the multi-threading. Thats not true - Prime simply IS much slower than MC15 and only sometimes on modern machines can at least live up to MC15 because of its ability to use more than one core/processor. Its sad that MC15 will never be able to do so.
Below a comparison between MC15 and the two modes of Prime2 on a slow single core (all with a 1000x1000 matrix splitted ten times in a row. Interesting the effect with split6, the routine that uses as few built-in commands and function calls as possible. This seems to show that PTC made the performance of the built-in routines even worse as the used to be in MC15.
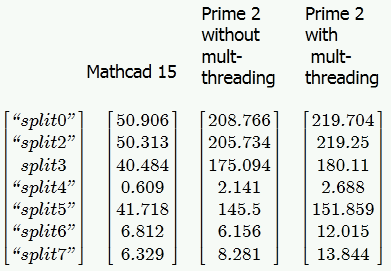
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
the figures are impressive. What about the idea splitting the problem in two and reuniting the results?
This allows the cores to work in parallel.
I will give it a try with Mathcad 15 starting two instances if I'm in need next time:
start instance 1
start instance 2
both calclulate
instance 1 writes results of the calc into prn.
instance 2 finishes and waits for the prn of instance 1 to be read
instance 2 re-unites the partial results doing the post processing...
May be that helps?
For PRIME the algorithm is different since within one worksheet you have more parallel processes.
stack the result matrices of one calculation on top of the other
I don't know whether I can use the same subprogram for this, to be called with different parameters, in contradiction to PTC's own example, may be the math kernel library used optimized that itself.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the figures are impressive.
You are speaking abou MC15 being quicker? We have seen that before and you found it out yourself on your i7, I think. If I remember right you reported for Prime2 similar values as with MC15 and I suspect thats due to the parallel processing cababilities. As you have reported about memory problems, too in some other threads, it could be better to stay with Prime as at last speed seems somewhat similar and there is the hope that the more modern Prime architecture would deal better with memory, has better garbage collection, ... But thats guessed/hope, not known, so you have to test for your own.
What about the idea splitting the problem in two and reuniting the results?
This allows the cores to work in parallel.
I will give it a try with Mathcad 15 starting two instances if I'm in need next time:
While (hopefully) each instance of MC will get its own core, they still will compete against memory. Hope this will not be a problem.
Another question would be how you manage instance2 to wait until instance1 has written its output file. Reading the file (which has to exist) in a loop until the last values/characters are a specific token would cost a lot of ressource. I guess that its not instance2 which will wait but thats you and you will then manually start the reunion process. The reunion of the large partial results will cost quite some time, too, so the benefit would be not that big.
But at the end you will have to try it with your problem, on your machine. All we know so far is to avoid built-in routines like "stack".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am noticing huge bottlenecks in Mathcad Prime 4 when splitting and flattening matrices when using the built in operator for row and built in function of stack.
If I explicitly redefine the operator and function as new functions I am seeing massive speed improvements. The speed is also affected by the type of value sent to a matrix. For instance, a string assigned to all elements of a 10000x4 matrix takes 32 sec to be split using the row operator. If I overwrite this it takes 0.094 seconds, no joke.
If I then flatten the resulting split matrix using the built in stack function, it takes 173 sec !!!!!!! vs 0.3 s if I do it explicitly.
What on earth is going on?
Also, if an integer is assigned to the matrix instead of a string the speed is massively reduced 0.011 secs vs 34 secs.
The reason for manipulating string matrices in this manner is of course to work with data sets.
Steve





