Minerr/nonlinear optimizing

[RichardJ]

In reference to this document: Minerr/nonlinear optimizing

Your equation for Function is wrong. For a least squares fit the error function should be the square root of the sum of the squares (or just the sum of the squares). You have the sum of the square root of the squares, which is equivalent to the sum of the absolute values. See my Function2 for the correct error function.

Having said that, the best way to fit a function to experimental data is to create a function that generates the vector of residuals: see my Function3. Feed that directly to minerr, and use the Levenberg-Marquardt option.

Minimizing Function gives an error (i.e. Function2) of 1721, 311, or 133, depending on the algorithm used

Minimizing Function2 gives an error (i.e. Function2) of 1628, 109, or 100, depending on the algorithm used

Minimizing Function3 using the LM algorithm gives an error (i.e. Function2) of 261

I'm not sure why the last option does not give an error as low as a couple of the other options, except to say it has to do with where the minimization ends. Using a vector of residuals with the LM algorithm, maybe it takes a slightly different path and gets trapped somewhere in a local minimum. Changing the guesses may help. Nevertheless, despite the fact that the error is slightly higher in this example, in general this is the best approach.

[RichardJ]

I played around a little, and it's super sensitive to the guess values. I'm not sure anything we have found is the true minimum, and I'm not sure any gradient method is the way to find the true minimum. Maybe simulated annelaing: Minimizing a Function using Simulated Annealing. I'm traveling in Europe at the moment though, so I'm not sure when I will find time to try that.

[mnori]

I would like to joint the discussion about Minerr Levenberg-Marquardt, since  I found me to some convergence issue, for some additional points:

1) It is possible to use relative deviations( |X-Xxep|/Xexp instead of residual ( |X-Xexp| (  in order to taking in account the variable absolute value) (?)

2)  It is possible to consider two ( or more)  weighted objective functions to be minimized in the same solve block or it is best to consider the sum of them ( a single boolean equation) (?)

3)  In order to check wheter Minerr has found a true minimum, it is possible to use the ERR function  alternatively to recalculate the objective function?

[RichardJ]

1) It is possible to use relative deviations( |X-Xxep|/Xexp instead of residual ( |X-Xexp| (  in order to taking in account the variable absolute value) (?)

Yes, it is just a weighted fit. For a true least squares fit the errors should all be of equal standard deviation. If the errors are independent of the magnitude of the data that means they should be unweighted. If the errors are proportional to the magnitude of the data then they should be weighted by 1/magnitude, which is what you propose.

2)  It is possible to consider two ( or more)  weighted objective functions to be minimized in the same solve block or it is best to consider the sum of them ( a single boolean equation) (?)

Yes, just stack the (weighted) residuals, or put them in two columns of a matrix.

3)  In order to check wheter Minerr has found a true minimum, it is possible to use the ERR function  alternatively to recalculate the objective function?

I'm not sure what you mean. The ERR function is a built-in variable, not a function, that gives you the error in the fit. When minerr stops iterating it has found either a flat area in the objective function or a minimum. There is no way to know which (other than by trying different guesses), and no way to know if it is the global minimum.

[mnori]

Thank you,

I am currently applying the Minerr Levenberg-Marquardt for the classical chemical engineering problem of fitting the pure component parameters of a volumetric EOS ( Equation of State ) versus experimental vapour pressure and liquid density. Since the equation is implicit on the density, depending on the initial values, Minerr could converge to a false minimum ( e.g. wrong root: vapor density). Could  the minimization problem be solved alternatively with Simplex algorithm type. Is this available in MathCAD?

[AlvaroDíaz]

Hi.

Not with Minerr.

With minimize, you can impose the adequate conditions inside the solve block with <, <= to the variables to ensure the convergence to the desired range. But then the problem is how to express the zero of the function. For a lot of problems works simply include abs(f(x,y,..))=0 or something about squares and related conditions. But for several variables it could be problematic.

With solve you can also include restriction over the variable domain, and don't need to prepare the function to solve too much. But, again, for several variables don't works for the general case, and need to use minimize with an optimized condition for f.

As comment, can't read the water data, mathcad says something about loss region when load the worksheet. But don't know if it is my problem, or others collabs have it.

Best regards.

Alvaro.

[mnori]

Hi Alvaro,

Thank you for your answer. The experimental data are copied and pasted as table from the following  Thermophysical Properties of Fluid Systems ( saturation properties -temperature increments ).

The attachment is analogue file for Benzene ( i.e. no association contribution ). Here the minimization algorithm works straightforward, so I think the convergence issues are related to the association contribution ( SAFT type ).

Your faithfully,

Massimiliano

[AlvaroDíaz]

Hi. I can't read the original data, problems loading the mathcad document, for the benzene too.

I copy some data, and what I can see is that the first solve block fails for some points, not all of them. So, guess you can "un-refine" the interval from NIST page, or reduce the whole interval for get some one where all data points gives a solution for the minerr block. See attached. Try also to change the solve method for quasi Newton or Conj-Grad. Also, try for TOL=CTOL=0.01. You have several variables, but for T in K and P in Pa this value is actually a very very small one.

You can identify points where the solve block fails.

Best regards.

Alvaro.

[mnori]

Hi,

Thank you for your indications. I will try to apply your suggestions. However the convergence of the solve block is not a "sufficient condition", if you see in most cases the two solutions coincide, while in case of benzene not, the first (0) representing the vapor, the second (1) representing the liquid, with the given reduced density initial values (  0.0001 and 0.6  ).

Your faithfully,

Massimiliano

[AlvaroDíaz]

Hi Massimiliano. Yes, you're right about the "sufficient condition" (<=), but it's a "necesary condition" (=>) for working the minerr block. And it's true what you say about the benzene too.

But I don't show the correct picture, playing with CTOOL make a nonsense mistake. Attached shows better what's I says: see the result for row 24 of the data.

Best regards.

Alvaro.

[mnori]

Thank you Alvaro,

I tried to change method, initial values and tolerances (  CTOL and TOL ).

The "on error" conditional function is very useful to analyse the Minerr loop convergence. I think that some convergence issues depends on the analytical form of the association contribution. In a previous thread for instance, it was found out that the second derivative has some numerical instabilities increasing the value of the association parameters ( Vaa and epsilonaa).Numerical issues with Symbolic Derivative Operators‌. Here I was trying to set the association parameters nihil in order to determine the critical parameters and to adjust them  for the fitting of the vapour pressure and liquid density.

Your faithfully,

Massimiliano

[RichardJ]

I've been traveling, so I only just got a chance to look at this. Could you please clarify why you think the water worksheet has a problem, but the benzene one does not.

Edit: Forget it. It's obvious when I look harder.

[mnori]

Just a consideration: The only difference between the two worksheets is that the Benzene uses an EOS that is a 7th degree polynomial equation in the density (eta) while the EOs in  Water.rev  is obtained  adding to this equation the so-called association contribution ( SAFT type ) due to Wertheim's Perturbation Theory.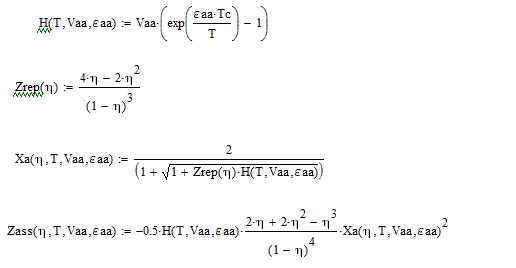

Overall there are eight (8) parameters.

Two (2) of them ( epsilon and bc ) are determined by solving the isothermal critical conditions,

the remaining six by minimizing the objective function in the Minerr Levenberg-Marquardt loop.

 

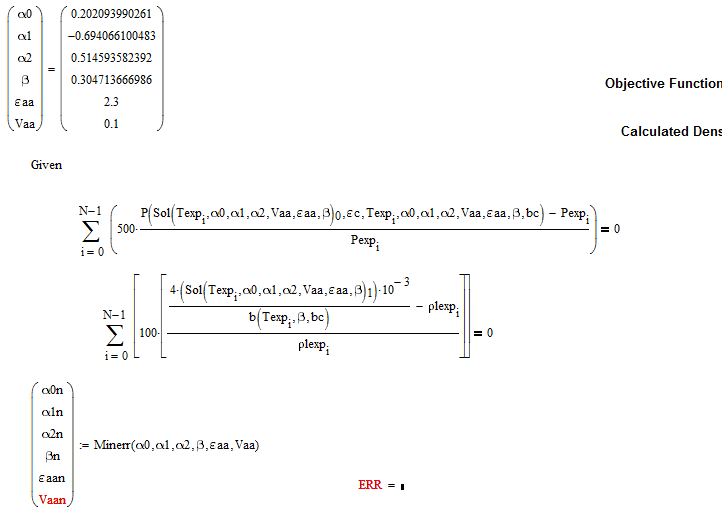
where the experimental data ( vapour pressure and liquid density ) are taken from the Matrix

:

[AlvaroDíaz]

Hi Massimiliano.

Before calling Sol inside the minerr block, ¿do you check that for all i don't have any error for Sol(Texp[i,alpha0,...)? I can't because my mathcad refuses to load your original data "Water" .

If that, you can try to eliminate the problematic rows from the data,as workaround, and then go with the actual issues for the minerr implementation.

Best regards.

Alvaro.

[mnori]

Hi Alvaro,

  By using the on error conditional function, I noticed that the number of critical rows for temperature depends on parameters and variable initial values. I have not tried to get rid of all the problematic rows, before entering the Minerr since in principle I would like to fit all the reduced temperature range [ about 0.4-0.9 ]. So when Minerr find an error in Sol , it stops the optimization?

I was thinking that the algorithm by changing parameters  values was able to converge to a solution.

Your faithfully,

Massimiliano

[AlvaroDíaz]

Massimiliano Nori wrote:

.... So when Minerr find an error in Sol , it stops the optimization? ...

Yep. Use the previous posted error detection with the "on error" command to discard problematic points from the data Water before use the Sol function inside the minerr block.

That's a rude workaround. You can try other techniques, like "un-refine" the interval, or something more elegant, but with those errors can't get a solution from minerr.

... I was thinking that the algorithm by changing parameters  values was able to converge to a solution. ...

No. After Sol was defined, can't modify it by changing anything. Actually that's uncomfortable to me, and I'm use some workarounds, but in Mathcad 11. Also, this is why I comment in the mathcad worksheet that, even can change TOL and CTOL before minerr block, isn't the best practice, just because Sol don't go to use them, and go to take the previous values.

Best regards.

Alvaro.

[mnori]

  No errors is found by the conditional function after changing parameters/variables initial values. It looks that some limitations are inherent in the model (?).

What ( if exists ) is the maximum computational time for the Minerr-Levenberg-Marquardt optimization loop? How the parameters are varied within the Minerr-Levenberg-Marquard loop ? What does implies if Minerr function stops before converging ( i.e. undefined variables )?

[AlvaroDíaz]

Hi Massimiliano.

Others are the experts in this algorithms, and hope can answer to you more precisely, but there are my answers:

No errors is found by the conditional function after changing parameters/variables initial values. It looks that some limitations are inherent in the model (?).

Maybe not, with the usual limitations of all numeric algorithms have enough.

What ( if exists ) is the maximum computational time for the Minerr-Levenberg-Marquardt optimization loop?

Usually programs with iterations don't eval the time, but use a counter for check if some MaxIters was rached. If that, program halts. Sometimes the programmer set the answer as the last approximation, but a good best practice is to notify an error. So, the time involved in the loop is variable, depending on the time that the functions and constraints take to eval. See this MaxIters in http://www.duke.edu/~hpgavin/lm.m

How the parameters are varied within the Minerr-Levenberg-Marquard loop ?

For that can check http://people.duke.edu/~hpgavin/ce281/lm.pdf‌

What does implies if Minerr function stops before converging ( i.e. undefined variables )?

Nothing. Can use more iterations, can modify guess values, can do a lot of things before discard a model. Or can use the best calculus method: always use first degree approximation, like in the Newton method. This is: all are rect lines or planes.

Best regards.

Alvaro.

[RichardJ]

What ( if exists ) is the maximum computational time for the Minerr-Levenberg-Marquardt optimization loop?

I'm nor sure of the details, but there is an upper limit. I suspect it's a maximum number of iterations rather than a time. Whatever the details are, the limit is high, and if it's reached then there is a problem with the optimization.

How the parameters are varied within the Minerr-Levenberg-Marquard loop ?

It's a downhill method. it starts at some point on the (multi-dimensional) error surface that is determined by the guess values. It then iteratively proceeds "downhill", i.e. to lower error, until it can't find a lower error. Ideally that would be because it reached a minimum (even more ideally, it would be the global minimum, but there is never any guarantee of that), but it could also stop because it reaches a discontinuity, a flat spot in the surface, or some other problem that stops it from finding a better solution. I posted the original paper that describes the algorithm here: Re: Why minimize not work in this Mathcad Prime 3.0 sheet?

What does implies if Minerr function stops before converging ( i.e. undefined variables )?

The "undefined variables" error message is useless, because it's the only error message returned by a minerr solve block. It could mean anything. It could really be an undefined variable (i.e. one or more variables do not have guess values assigned, and/or some other variable is undefined), or it could be a divide by zero problem, or some part of the error function can't be evaluated for some other reason, or just about anything else.

[mnori]

Thank you Alvaro and Richard for the clarifications.

In order to determine the error source of the "undefined variable", is it possible to lively monitor the parameters "guess" values in each iteration of the Minerr solve or to have an indication of the extent of their variation at a given step?

Furthermore in some cases as in the print-out I have attached before the conditions in the solve Block were not reached ( objective function <CTOL ( e.g.0.001 ) but not error message was returned.

[RichardJ]

In order to determine the error source of the "undefined variable", is it possible to lively monitor the parameters "guess" values in each iteration of the Minerr solve or to have an indication of the extent of their variation at a given step?

No, you do not have access to the values of the parameters at each step. However, if minerr fails then more often than not it's immediate, on the first iteration. For example, the guess values mean that the objective function cannot be calculated. This is something you can check for outside the solve block.

Furthermore in some cases as in the print-out I have attached before the conditions in the solve Block were not reached ( objective function <CTOL ( e.g.0.001 ) but not error message was returned.

Unlike Find, Minerr stops when the objective function changes by less than CTOL, not when the objective function is less than CTOL.

[mnori]

"No, you do not have access to the values of the parameters at each step. However, if minerr fails then more often than not it's immediate, on the first iteration. For example, the guess values mean that the objective function cannot be calculated. This is something you can check for outside the solve block."

You mean that it is possible to evaluate the objective function outside the solve block for guess values of the parameters (?) 

"Unlike Find, Minerr stops when the objective function changes by less than CTOL, not when the objective function is less than CTOL."

And what does TOL  represent in the Minerr solve?

[RichardJ]

You mean that it is possible to evaluate the objective function outside the solve block for guess values of the parameters (?) 

Yes

And what does TOL  represent in the Minerr solve?

I don't think it represents anything.