Skip to main content
V
24-Ruby IV
ValeryOchkov24-Ruby IV
24-Ruby IV
April 18, 2019
Solved

Minimize: 6 variables and 4 equations

  • April 18, 2019
  • 1 reply
  • 2768 views

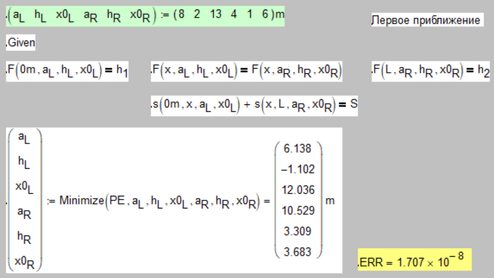
One mathematician has said me that if you have 6 parameters in the minimize function - you must have 6 or more equations in this solve block. I have only 4! Is it correct?

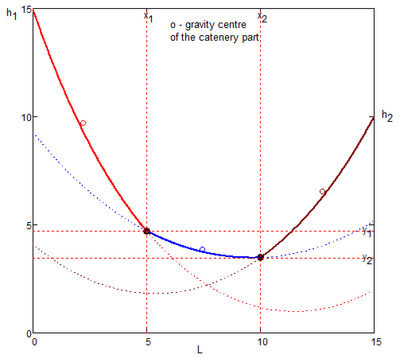
See please one interesting problem in attach!

Thanks! 

Best answer by Werner_E

The less equations (or the more variables) the more solutions, resp. the more degrees of freedom.

So its easier for the solver to find a solution but this solution will heavily depend an the choice of the guess values.

As you can see below you can check the quality of the solution by evaluating the built-in variable ERR (its exactly this variable which Mathcad tries to minimize) and you may consider adding some additional constraints like aL>0 or the like, to avoid unwanted solutions.

B1.png

B2.png

B3.png

1 reply

W
Werner_E25-Diamond IAnswer
25-Diamond I
April 18, 2019

The less equations (or the more variables) the more solutions, resp. the more degrees of freedom.

So its easier for the solver to find a solution but this solution will heavily depend an the choice of the guess values.

As you can see below you can check the quality of the solution by evaluating the built-in variable ERR (its exactly this variable which Mathcad tries to minimize) and you may consider adding some additional constraints like aL>0 or the like, to avoid unwanted solutions.

B1.png

B2.png

B3.png

    V
    24-Ruby IV
    ValeryOchkov24-Ruby IVAuthor
    24-Ruby IV
    April 18, 2019

    Thanks, Werner!

    I think (guess) it (degrees of freedom) is more for the Find not for Minimize/Maximize Function.

    See please the problem with 9 variables and 5 equations

    MM.png

    W
    Werner_E25-Diamond I
    25-Diamond I
    April 18, 2019
    @ValeryOchkov wrote:

    Thanks, Werner!

    I think (guess) it (degrees of freedom) is more for the Find not for Minimize/Maximize Function.

     

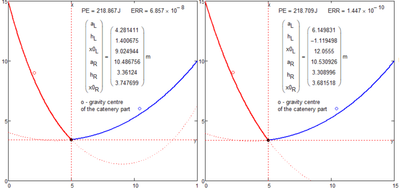
    It applies in a similar way to a solve block with "minimize", too.

    The less constraints and the more variables to change, the more possibilities to find different but equally good solutions. Ever so often in such cases depending on the equations given Mathcad possibly won't even change the guess value of the one or other variable given.

     

    In your new sheet its quite interesting that we get the very same results using "find" and without referencing PE in any way!?

    B.png

    Terms & ConditionsCookie settingsAccessibility statement