Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Minimum value of the function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Minimum value of the function.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Loi Le,
try this sheet which uses the Minimize function
Raiko
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks for your response, Raiko Milanovic.
Best Regards,
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its NOT a minimum - see my other post.
Its an "artificial" step at 0.5 because of Mathcads try making a function unique which is not unique.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
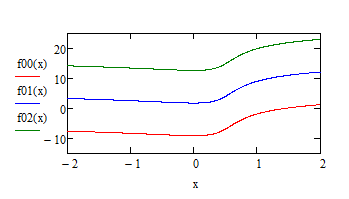
Complex numbers and logarithms - a never ending story 😉
The graph you provided is only one of an infinite number of representations of your function f.
The reason is the second term which is the natural logarithm of a complex number with length 1. That logarithm of that kind of number is a complex number whose real part is zero (what is "rein imaginär" in English?).
But - the logarithm function is not unique over the complex numbers. The log of a complex number has infinite values, all of which have the same real part and the imaginary part differs by multiples of 2*pi. This, in your f(x), is then multiplied by sqrt(-3), making it a real number.
So in your function you can chose at any point x to add a multiple of 2*pi*sqrt(3) (the second log) and go on from there jumping from one leaf of the 4-dim log plane to another. Mathcad does this at x=1/2 because the arg function defaults to values from -pi to +pi. At x=1/2 the argument of the complex number in the second log would go beyond pi and so mathcad subtracts 2*pi - creating artificially the step you see in the graph. You may notice that the difference between the two "cusps" is exactly 2*pi*sqrt(3).
So if you forbid those kind of "jumps" and demand continous graphs, the answer to your question (minimum) is: its at x=0 and is pi/sqrt(3) plus any multiple of 2*pi*sqrt(3).
See below three (out of an infinite number of) continuous representations of your function: