Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Mismatch calculation result
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mismatch calculation result
Hi,
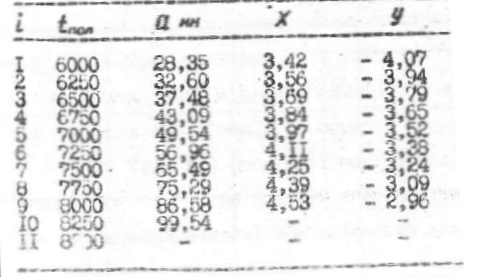
The Mathcad document have some calculations from the old article. The article says that all the calculations are done on a computer. However, my results do not coincide with those shown in the article. On the screenshots you can find input information (a, t), the formula for calculating the value (x, y, b_0, b_1). I have tried to carry out calculations with different accuracy, but the result is still different. Maybe I missed something?
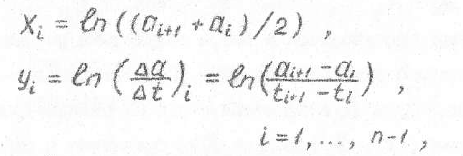
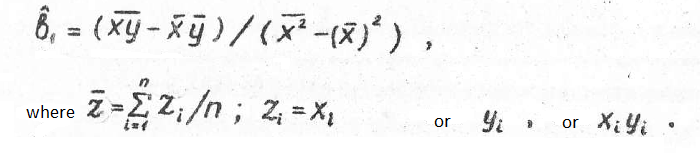
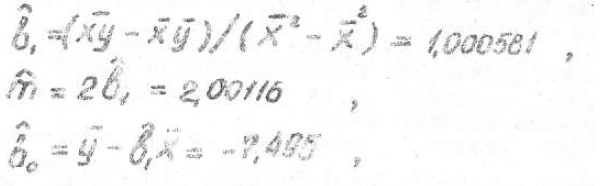
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I get the very same results as shown in your sheet and the results are pretty close to those given in the handwritten screenshots of yours. Difference for b_1 is just 7*10^-4, for example.
The reason for that small discrepancy could be that the values of a are given rounded to 2 decimals but the original calculations may have been done with more accurate values. So we can't duplicate the calculation exactly without knowing the accurate values of a. You may also notice that even the values of x and y are somewhat different at the second decimal place which is also a hint that the original calculation was not done with the given, rounded values of a.

EDIT: You may also check using Mathcad's built-in functions:
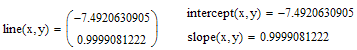
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you. Too frequent rounding calculations lead to such difference results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have checked this every way I can think of, and I can't figure out how the author got that number. I even tried using the symbolic processor to restrict the numerical precision of the calculations to a few decimal places, but the answer is never greater than 1.
As an aside, you can use the mean function, as Werner shows, to make the expression rather more compact. Going one more step, the expression is the covariance of x and y divided by the variance of x, so you could write cvar(x,y)/var(x). But of course, as Werner also points out, that's just the slope of a linear regression, so you could just write slope(x,y) ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. Yes, I know about the possibility of using the built-in functions here, but I need to show this algorithm for a person who is not familiar with Mathcad. I think the main problem here is the calculation with too frequent rounding of intermediate calculations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think the main problem here is the calculation with too frequent rounding of intermediate calculations.
Maybe, but the float keyword does exactly that, and did not yield the same results. Maybe the author rounded in a different way though.





