Moessner's theorem

[AlfredFlaßhaar]

A friendly hello in search of help,

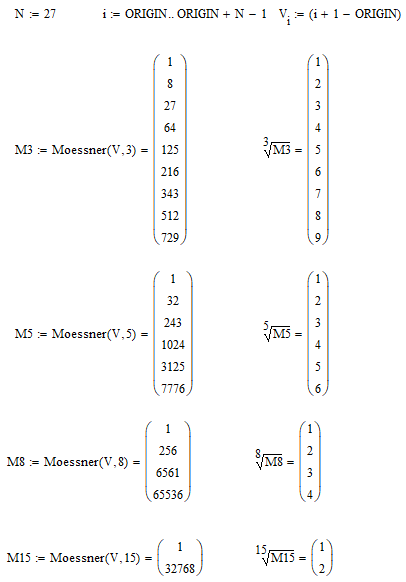
Moessner's theorem is well known to me from number theory. It is vividly described in https://en.wikipedia.org/wiki/Moessner%27s_theorem and https://thatsmaths.com/2017/09/14/moessners-magical-method/. I would now like to experiment numerically with this sentence for a change in "practice". Starting from the sequence of natural numbers 1, 2, 3 ... a subsequence is removed from it according to an essentially arbitrary rule (e.g. every third number, square numbers, prime numbers, ...). The sequence of partial sums is formed from the remainder. With the sequence of the partial sums, the procedure is repeated with the same selection rule until it logically breaks off. And that's my programming problem. In MC14 I can't get a handle on the selection, the sequence of partial sums and the repetition as an algorithm, it was always vector nonsense that I don't want to publish here.

It would be helpful if I could get a program skeleton with hints using the example "Selection of every third natural number".

Kind regards, Alfred Flasshaar

[Werner_E · Accepted solution]

Here is a program which should do the job

Examples:

[AlfredFlaßhaar]

That's it, thanks a lot.

[Werner_E]

You are welcome!

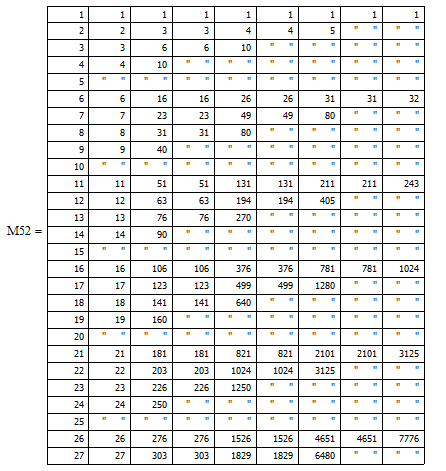
I added a modification so the intermediate steps can be seen

[AlfredFlaßhaar]

Somehow it gives pleasure to see how the numbers obediently behave according to theory 🙂 . One more question, please: How are square numbers or prime numbers sorted out instead of every "n´th" natural number? How to enter any choice in your program?

[Werner_E]

I would use separate programs like the removeEveryNth( ) to remove primes and squares.

The programs would run through the vector, test each number for the desired characteristic/property (prime, square, ..) and acts accordingly.

Testing for primes or squared could be done in further separate programs (divide and conquer). For not too large matrices I guess that brute force would suffice - that is trying for every (odd, in case of primes) integer i up to the root of the number n in question if mod(n,i)=0 or if n/i = trunc(n/i), or in case of squares, if i^2 = n.

To make a choice in my program, we could turn the second argument into a 3x1 vector. If the first entry is larger than 1 it would have the very same meaning as the current argument n, otherwise removeEveryNth( ) would not be called. If the second entry is non-zero, all squares could be removed and the third entry in this argument vector would do similar for the primes.

So one program could be used for all.

Would it make sense to remove, lets say, every third number AND every prime? If so, the order of the removals would make a difference.

[AlfredFlaßhaar]

Thanks again for the help and explanations. Is it possible in an uncomplicated way to set the selection in your program to the (6*k+1)´th or (6*k+5)´th separately for k = 1, 2, ...? This means: In the first case, every 7th, 13th, 19th, ... and in the second case, every 5th, 11th, 17th, ... number is to be sorted out. If this is possible, I ask for your support, as I am not able to program in MC.

[Werner_E]

I am not sure how your new suggestion should actually work, when the iteration should stop, etc.

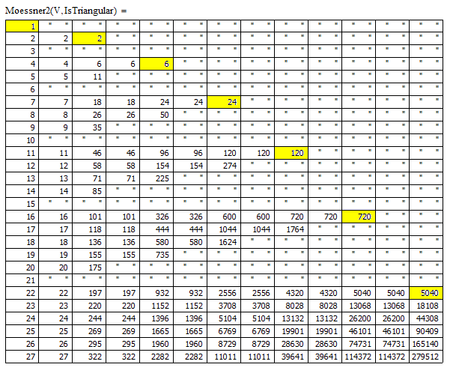
In the meantime you may have fun with the additions I added to the last version, e.g. getting the series of factorials by removing the triangular numbers

Not sure if removing the squares or Primes would lead to something interesting

Iteration in Moessner2 stops when no change in the series occurs anymore - there may be better ways ...