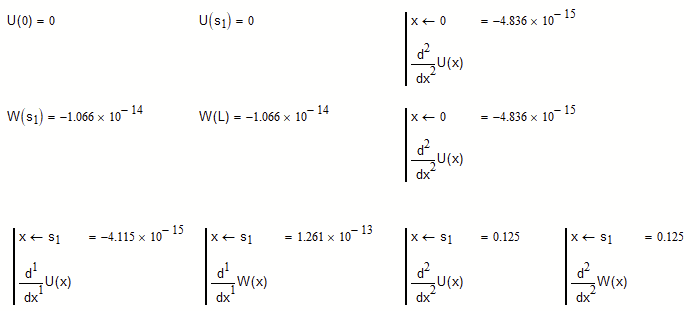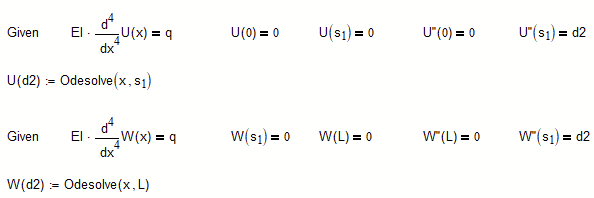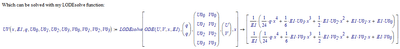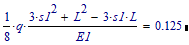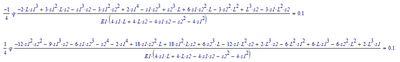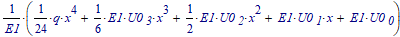Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Multiple ODE's in MathCad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Multiple ODE's in MathCad
Hi guys,
I have a question..
I modelled a 4th oder ODE in MathCad which works smoothly..
But when I tried to upgrade the script into (a system of ODE’s) 3 or 4 ODE’s, I couldn’t get it well working.
Note that I checked the boundary/matching conditions and they are correct. So something else could be wrong.
I’ve included the file in the mail.
Would you like to help me here?
Thanks in advance!
- Labels:
-
Mathcad Usage
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The Odesolse finction cannot work with a boundary problem.
For this there are others tools. The Shot method for example (a programming). Or the bvalfit etc function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Valery,
Could you help me with an example?
I'm not sure how the bvalfit works..
Thnx in advance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From "Help Center" - "Deriving Initial Conditions for an ODE": https://support.ptc.com/help/mathcad/r8.0/en/#page/PTC_Mathcad_Help/deriving_initial_conditions_for_an_ode.html
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Attached is an attempt using the shooting method. I've split it into two sections; one from x = 0 to x = s1, and one from x = s1 to x = L, matching the specified boundary conditions at x = s1.
Unfortunately, it doesn't get one of the final boundary conditions correct (that for W``(L)).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Alan,
I would like to thank you very much for your help, at least I'm a step further now.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hallo Alan and everyone,
Firstly, thank u Alan and eveyone who gave his time for this.
Idon't know how to work with guesses and I don't even understand it.
But also a question, I thought I know the exact values for the boundary/matching conditions, so why do we need guess values?
Maybe I lack the experience here, but previously I used to program similar models in Maple but here (in MathCad) it does'nt work..
Any Idea?
Thanks in advance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This solution might not be satisfactory as it does not use a solver for a differential equation, but at least its a solution.
You are asking for two polynomials of fourth order which are zero at 0 and s1 resp. s1 and L, have their second derivative at 0 resp. L to zero and have matching first and second derivatives at the joint position s1.
Actually this means 10 conditions for 10 variables (the coefficients of the polynomials) which you can either solve using the symbolic solver or using a numeric solve block. Of course, as we know the fourth derivative of both functions being q/EI we could set the coefficient of x^4 in both functions to q/(24 EI). But I decided to let Mathcad do the job 😉
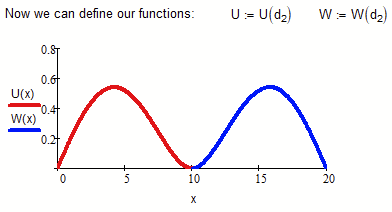
Here is what Mathcad came up with
As you can see, the necessary conditions are met (apart from minor numerical inaccuracies):
i still have no idea how to get odesolve to come up with this solution, though.
MC15 sheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So here is a method which uses odesolve - unfortunately still not the "natural" way.
First we use a separate solve block with "odesolve" for U and for W and turn it into a function of the value d2 of the second derivative at x=s1.
The only condition not met when we calculate the functions using the same value for d2 is that we also want the first derivatives at s1 to match.
So we define a function to calculate the difference of the first derivatives at s1 for any value of d2
and use it in a solve block with "find" to iterate the values of d2 until we arrive at a value where the first derivatives are equal.
Wish it would work in one go basically the way you had set it up, but it looks like Mathcad isn't capable enough to do so. However, I would be happy to be proven wrong.
Mathcad15 worksheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi mate,
How wonderful is this update..
Thanks so much for your time and efforts
I'll check it and let u know.
Thx,
Mohamed
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
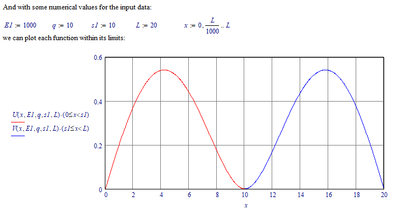
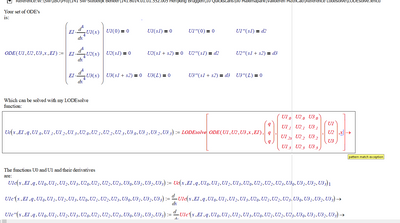
With reference to https://community.ptc.com/t5/Mathcad/Toolbox-Solving-Ordinary-Differential-Equations-symbolically/m-p/689336#M192090
Your system of 2 ODE's can be solved as follows:
Note that the value of d2 is:
which corresponds to what @Werner_E found.
If you want to run this in Mathcad 15, be sure to take the proper LODEsolve reference file,
you need to replace the LODEsolve.mcd with LODEsolve.xmcd
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
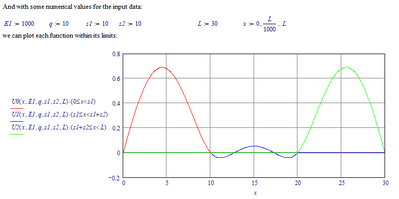
Oh, and in case you wonder if it can be done with three sections...
Hoping/assuming I have set the proper initial/boundary conditions, here goes:
And in case you're wondering about d2 and d3... they are 0.1 each. That is respectively:
The Mathcad 11 file is attached again.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Luc,
Thank you very much for this amazing effort. I appreciate it
Just one issue.. when I download your files, they don't run (calculate). That graph above doesn't plot any outcome!
I see the screenshot you included, so I know it should work but maybe it has to do with the version I'm working with (MathCad 15)..
Any idea how I can get out of this dilemma?
Thanks in advance 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes. How about pressing the [F9] key every now and then, to calculate the sheet up to the point where it's being displayed. Or press [Ctl-F9] to calculate the entire sheet...
I generally have Autocalculation switched OFF in my files. That way I can edit the expressions without being hampered by Mathcad trying to calculate every change I make, and slowing down my editing.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
With each step I do consider that..
But looks like my version (MathCad 15) doesn't like some functions/expressions as below:
The function LODESOLVE is not recognised along with some expressions in red..
Any idea why?
Something to do with the version I'm using maybe?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You probably forgot to change the include file. At the top of my sheet is a reference to LODEsolve.mcd, that is the file that contains the definition of the function LODEsolve. Without that include file, the sheet will not work. And there are two incarnations of the LODEsolve file, one is LODEsolve.mcd (that runs in Mathcad 11), the other is LODEsolve.xmcd (that runs in Mathcad 15). LODEsolve.mcd will not work in Mathcad 15, and LODEsolve.xmcd will not work in Mathcad 11.
You have to get the LODEsolve.xmcd from this thread:
Scroll to the bottom of that thread to grab the latest version of LODEsolve.xmcd
Save that file on your computer, and replace the present reference to LODEsolve.mcd with a reference to the LODEsolve.xmcd file.
Success!
Luc
P.S. Also note that the function for solving LODE's is named LODEsolve, not LodeSolve nor LODESOLVE.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Luc,
I did that, and I'm a step further now..
But I ran into an error (pattern math exception)..
Probably the symbols?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I assume that the example file LM_20201019_LODEsolve.xmcd in the other thread (still) works for you in Mathcad 15. That means that LODEsolve is still able to solve a set of differential equations, but is having problems with your specific set.
I can't debug at the moment, because I have no access to Mathcad 15.
Fortunately you actually do not have a set of differential equations, but a single differential equation that is split over multiple regions of the running variable. The general solution for that differential equation is a single one:
for the first region, then replace U0 with U1 for the second region and with U2 for the third (and so on if you like).
The attached solution file uses this property to solve your problem.
See if it works for you.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A slightly more compact implementation, which is easier to expand to more sections is attached below.
Success!
Luc