Nachträgliche Definition nach Anwendung von solve

[PiaLangoth]

Hallo zusammen,

beim Arbeiten mit Prime 3.1 ist bei mir wieder einmal eine Frage aufgetreten.

Eine kurze Beschreibung was ich machen möchte:

Ich möchte alle Schnittpunkte von 2 Ellipsen berechnen und zwar mit dem symbolischen Schlüsselwort "solve".

Ich habe nun die Gleichung aufgestellt, gleichgesetzt -> zunächst nach dem 1.Parameter x aufgelöst -> das Ergebnis in die Gleichung eingesetzt und möchte nun nach y auflösen (siehe auch angehängtes Mathcad-File). Wenn ich die Gleichung nach y symbolisch auflösen möchte, dann beginnt Mathcad zu rechnen, rechnen, rechnen.... und kommt zu keinem symbolischen Ergebnis.

Meine nächste Idee war die Schnittpunkte nicht allgemein zu berechnen, sondern die Parameter der Ellipsengleichungen vorher zu definieren (also x1, x2, y1,y2 usw.) und dann nach y aufzulösen. Das funktioniert sehr gut (siehe Mathcad-File) -> ich bekomme alle Schnittpunkte heraus.

Jetzt ist es aber so, dass ich nicht nur 2 Ellipsen schneiden möchte, sondern 20 oder mehr hintereinander (also immer 2 verschiedene Ellipsen miteinander schneiden, aber das ganze 20/30 mal). Meine Idee war nun, dass ich jeweils einen Vektor für die jeweiligen Parameter aller Ellipsen erstelle, also einen Vektor x1, x2 usw. . Ich habe gehofft, dass ich "solve" dann auf alle Einträge des Vektors anwenden kann und somit alle Schnittpunkte von je zwei Ellipsen als verschachtelten Vektor zurückbekomme. Dazu habe ich eine Bereichsvariable definiert, deren Bereich sich aus der Anzahl der zu schneidenen Ellipsenpaare ergibt (in meinem Bsp. = 2) und dann habe ich versucht "solve" elementweise anzuwenden. Das funktioniert, aber jetzt mein Problem: Ich kann das Ergebnis keiner Variablen zuweisen. Ich habe alles versucht (als Funktion in Abhängigkeit vom Bereich, als Matrix, usw.), ich bekomme immer eine Fehlermeldung bzw. ein "undefined". Hat jemand eine Idee ob/wie das in Prime funktioniert? Ich habe es auch in Mathcad 15 versucht, dort funktioniert die Zuweisung! Meine letzte Hoffnung war, dass ich das Mathcad 15-File nach Prime konvertieren kann -> die Konvertierung hat aber genau bei dieser Zeile fehlgeschlagen! 😞 Hat jemand eine Idee dazu?

Danke im Voraus für eure Hilfe!

[Werner_E]

Leider kann ich Dateien im Format P3.1 nicht lesen, nur solche im Format 3.0 und niedriger. Es gibt aber keinen Konverter und P3.1 kann auch nicht im "älteren" Format speichern - Thats PTC.

Die Schilderung klingt nach einer Verwechslung von Bereichsvariabler und Vektor.

Man kann eine Bereichsvariable einer Funktion als Argument vorsetzen und bekommt etwas zurück, das wie eine Vektor aussieht, aber keiner ist und sich daher keiner Variablen zuweisen lässt und sich auch sonst jeder Weiterverwendung widersetzt. Die Lösung besteht in der Regel darin, die Bereichsvariable durch einen echten Vektor zu ersetzen. Dieser kann dann der Funktion als Argument vorgesetzt werden - der Funktionsaufruf sollte dabei vektorisiert werden.

Ein fauler, aber sehr bequemer Trick, eine Bereichsvariable in einen Vektor zu verwandeln besteht darin, eine inline-Evaluation durchzuführen. Also etwa x:=1,3..8= zu schreiben. Das nachfolgende = durchläuft die Bereichsvariable und liefert einen echten Vektor zurück. Das Thema kommt hier im Forum sehr häufig auf und es gibt auch eine ganze Reihe von Routinen, die immer wieder gepostet werden, um einen Vektor bequem erzeugen zu erzeugen bzw. eine Bereichsvariable ohne den obigen faulen Trick in einen Vektor umzuwandeln. Nicht alle, aber die meisten davon funktionieren auch mit Prime.

Was mich aber irritiert ist, dass du schreibst, dass ein entsprechender Aufruf im Mathcad 15 funktioniert hat. Die Problematik Bereichsvariable vs. Vektor besteht dort aber genau so.

Kannst du vl die MC15 Datei schicken (die Stelle, die in Prime Probleme macht bitte markieren) und eventuell auch einen Screenshot oder einen PDF-Print von der P3.1 Datei.

Besten Gruß

Werner

[Werner_E]

Noch eine Anmerkung dazu:

Ich sehe ja leider nicht, was du in deiner Datei machst und in welcher Form die Ellipsengleichungen gegeben sind. Aber ich gehe davon aus, dass Gleichungen in Parameterdarstellung weniger Probleme machen würden und du schreibst ja auch, dass du eine Gleichung nach x auflöst. Ich nehme daher an, dass es sich um implizite Gleichungen in kartesischen Koordinaten handelt.

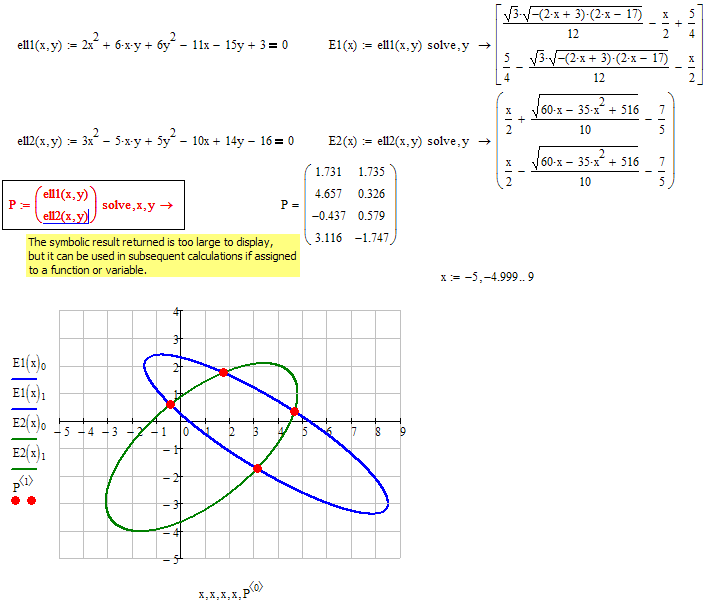
Ich habe mal so ein Beispiel in MC15 nachgestellt und direkt symbolisch lösen lassen. Es dauert tatsächlich eine kleine Weile, aber so extrem lang nun auch wieder nicht - ich schätz so 10-15 Sekunden. Ist aber auch nur eine der beteiligten Zahlen mit einem Dezimalpunkte versehen, so schaltet die Symbolik automatisch in den float-Modus und das Ergebnis ist sofort da.

Mathcad liefert den "Fehler", dass der Lösungsausdruck zu lang sei, um ihn darstellen zu können. Nichtsdestotrotz kann das Ergebnis aber problemlos numerisch ausgewertet und zB in der Zeichnung verwendet werden.

Ich füge einen Screenshot bei und häng die Datei dran - vielleicht hilft es ja.

Anm.: Die beiden Funktionenvektoren E1 und E2 mussten nur für die Zeichnung erstellt werden, da Mathcad leider leider keine Funktionen in impliziter Darstellung plotten kann. Deshalb auch die sehr dicht zum Plotten verwendete Bereichdsvariable x.(sie heißt x. und nicht x, um x auch nachher noch als undefinierte freie Variable zur Verfügung zu haben. x. sieht in MC15 wie ein normales x aus.)

LG

Werner

[PiaLangoth]

Hallo Werner,

danke für dein ausführliche Antwort!

Ja das habe ich mir schon gedacht, dass es hier bei mir zu einer Vermischung von Bereichsvariablen und Vektoren kommt!

Da du mein Prime 3.1 File nicht öffnen konntest habe ich eine Screenshot davon angehängt!

Danke auch für dein Beispiel. Was ich aber machen möchte (um bei deinem Beispiel zu bleiben): Ich möchte die beiden Ellipsen ell1 und ell2 nicht für konkrete definieren, also nicht 2x^2+6*x*y usw sondern A*x^2+B*x*y, da ich ja die Werte der Ellipsen variieren möchte. Jedoch stößt Mathcad bei mir da an seine Grenzen, ich bekomme kein "allgemeines" Ergebnis heraus. Darum war mein nächster Ansatz anstelle von einzelnen Werte für A, B usw. definierte Vektoren zu verwenden. Hier tritt dann aber das Problem mit der Zuweisung auf. Gibt es für mein Problem eine Lösung? Oder muss ich wirklich jedes mal, wenn sich die Ellipsenparameter ändern, erneut solve aufrufen?

Danke für die Hilfe!!

[Werner_E]

Ja, ich denke ich realisiere das Problem. Und e scheint nicht an Bereichsvariable versus Vektor liegen.

Ich werds mir später genauer ansehen, aber ich fürchte, dass es keine einfache Lösung geben wird.

In Mathcad 15 konnte man eine symbolische Auswertung noch lokal in ein Programm reinkopieren und könnte damit deine symbolische Auswertung in eine Funktion mit den Ellipsenparametern als Argumente packen. Damit gabs zwar auch immer wieder Probleme, weil die Ergebnisse einer solchen Funktion nicht "normale" numerische Werte Werte waren und zB nicht zum Plotten verwendet werden konnten. Abhilfe schaffte da eine neuerliche Zuweisung mit numerischer inline-Evaluation.

In Prime ist aber die lokale symbolische Auswertung in einem Programm überhaupt nicht mehr möglich, bei der Konvertierung älterer Programme wird nur ein Bild des Programms in das Prime-File übernommen und es enteht beim Versuch das MC15 Konstrukt zu realisieren dann der von dir beschriebene "undefined" Error.

Ich fürchte daher, dass mithilfe der Symbolik in Prime keine Lösung zu erzielen sein wird.

Eine numerische Lösung mit einem Lösungsblock liefert aber je nach Schätzwert nur eine Lösung. Man kann den Lösungsblock zwar in eine Funktion wandeln und auch den Schätzwert als Argument übergeben, die Frage ist aber, ob es möglich ist, die Sache so mit "geschickten" Schätzwerten zu automatisieren, dass immer alle Lösungen gefunden werden.

Valery hat ja gerade auf eine kleine Animation verwiesen, die an einem Beispiel zeigt, wie die Wahl der Schätzwerte das Ergebnis beeinflusst - es ist nicht immer eindeutig vorhersehbar.

Sind deine Ellipsen immer so beschaffen, dass die Achsen parallel zu den Koordinatenachsen liegen, so wie das dein Screenshot zeigt?

Und ist die halbe Hauptachsenlänge a bei beiden Ellipsen auch immer gleich?

Benötigst du nur die reellen Lösungen oder auch die nicht-reellen?

In MC15 könnte man ja auch mit einem Lösungsblock alle Lösungen erhalten, indem man diesen symbolisch auswertet, aber in Prime ist ja leider die symbolische Auswertung eines Lösungsblocks auch nicht möglich.

Werner

[Werner_E]

Ich hab mich nun länger damit beschäftigt (siehe beigefügte Datei) und fürchte, dass es tatsächlich keine Lösung unter  Verwendung der Symbolik gibt. Jedenfalls keine, die mir einfallen will.

In die funktionierende Variante mit dem Lösungsblock müsste man noch einiges an Hirnschmalz und Arbeit investieren um sicherstellen zu können, dass für beliebige Angaben immer verlässlich alle vier Lösungen gefunden werden.

In Mathcad 15 wär die Sache vermutlich schon längst gegessen 😉

Werner

[ValeryOchkov]

One animation

Video Link : 2418

[PiaLangoth · Accepted solution]

Hallo Werner,

ich hab es geschafft! Ich kann die Berechnung auch mit Vektoren in Prime durchführen! (siehe Anhang)

Meine zielführende Idee war schließlich, dass ich das Problem auf ein "symbolisch in Mathcad Prime lösbares Problem" herunterbreche.

Im Grunde ist das Ergebnis, dass man erhält, wenn man 2 Ellipsen gleichsetzt und nach einem Parameter (bei mir x) auflöst, ein quadratisches Polynom für den 2.Parameter (bei mir y). Ich habe mir dann aus dem erhaltenen Polynom die Koeffizienten für y^0,y^1,y^2 extrahiert (mit coeffs) und mit einem "vereinfachten" quadratischen Polynom B3*y^2+B2*y+B1 weitergerechnet. Dieses quadratische Polynom habe ich dann in die 2.Ellipsengleichung eingesetzt -> das ergibt ein Polynom 4.Ordnung. Dann habe ich wieder dasselbe wie vorher gemacht: die Koeffizienten zu y extrahiert und schließlich das "vereinfachte" Polynom y^4+C4*y^3+C3*y^2+C2*y+C1 =0 nach y mit solve symbolisch aufgelöst -> und das funktioniert in Prime!! Dann brauchte ich nur mehr die Koeffizienten "richtig" zu definieren, Parameter für die Ellipsengleichungen definieren und in die Lösung des Polynoms 4.Ordnung einsetzen... und mit dem Vektorisierungspfeil funktioniert das jetzt natürlich auch für Vektoren!

Puh...das war ein steiniger Weg, aber es funktioniert.

Danke für deine Hilfe!

Viele Grüße,

Pia

[Werner_E]

Schön, dass du es doch noch geschafft hast, eine für dich passable Lösung zu finden.

So scheint es eben die einzige Möglichkeit zu sein, die Aufgabe so mundgerecht vorzubereiten, dass auch die recht brustschwache Mathcad-Symbolik sie allgemein zu lösen imstande ist. Das ist schade, weil natürlich in anderen Fällen u.U. nicht möglich.

LG

W

[Werner_E]

Third and last one for now

Has anybody an explanation for the following weird effect?

To speed up calculation I tried to force the symbolics into float-mode by using the "float" keyword before the "solve" keyword and got an "Illegal operand" error !? Using float after solve works, but has of course no positive effect on calc time, as the solving part is done in exact mode.

A workaround is to use substitute,x=1.0*x which speeds up calculation as desired.

BTW, it is not advised to use "float,3" as shown above, because this affects not only the display of the result but means that the whole calculation is done with 3 digit precision only. So you will lose accuracy.

Werner