We are aware of an issue causing pages to load incorrectly for some users and expect a fix soon. Sorry for the inconvenience.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
New oval - an ellipse^ellipse
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
New oval - an ellipse^ellipse
I would like to plot (to animate) an oval - an ellipse with one focus as a point and second - an ellipse.
See about this problem Symmetry | Free Full-Text | A New Ellipse or Math Porcelain Service (mdpi.com)
But I have problems - tee pics and Mathcad 15 in attach.
One solution in SMath
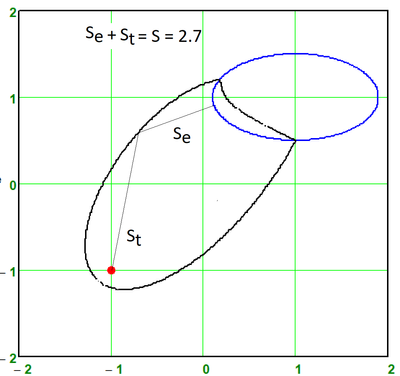
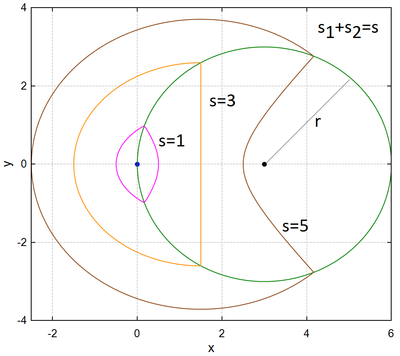
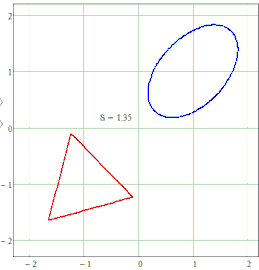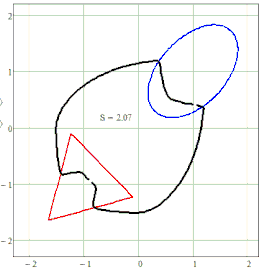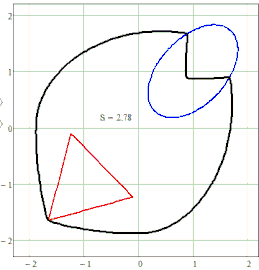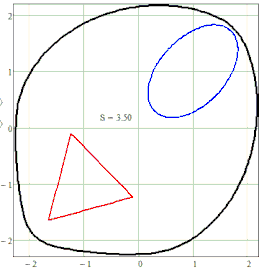
So, an ellipse and a hyperbola can be specified either through a focus with a directrix, or through a pair or more foci. But the focus can be not only a point, but also... a circle, and an ellipse and a hyperbola can be crossed and get an ellipsohyperbola.
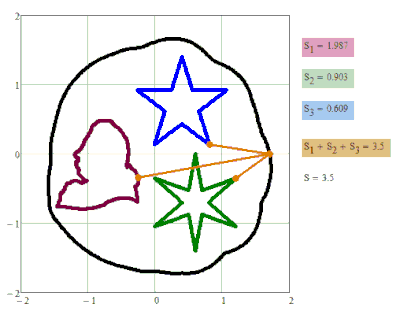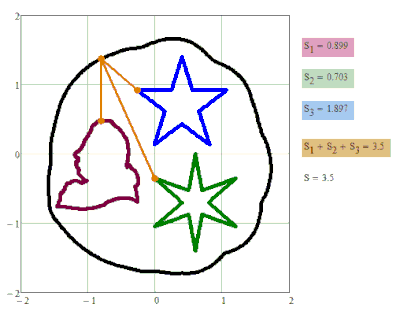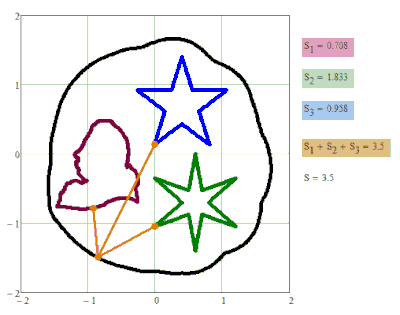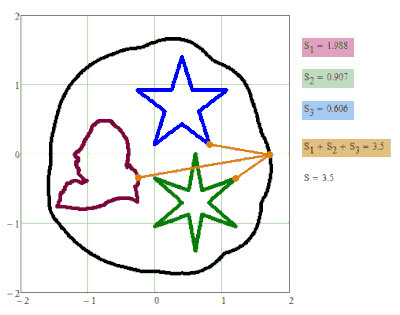
Figure shows a family of closed curves, which can be called these same ellipsohyperbolas. These are ellipses, in which the first focus is a traditional point, and the second focus is a circle. Outside the circle we have ordinary ellipses, and inside the circle we have branches of a hyperbola. This can be verified not only visually, but also mathematically - inside the circle, addition (ellipse) turns into subtraction (hyperbola). The ellipse (oval) on the border of the circle turns into a hyperbole at an angle and can finally bring harmony into the soul of the poet - see the divertissement epigraph. If you smoothly change the S parameter, you get an animation - a small green snake (a straight line segment between the left focus and the left edge of the circle) predatory (see the second name of the divertissement) swallows the circle in much the same way as a boa constrictor swallows a rabbit. At the end of this process, the ellipsohyperbola becomes a rather plump ellipse.
Help please!
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah yes, I now remember your post on porcelain manufacturing. There may be easier ways to create irregular ovals, but why not.
It's a little questionable, though, whether creating plates for the Fields award ceremony is a viable business model 😉
Maybe it could be made more interesting for a broader market by personalization using a silhouette 🙂
🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem lies in he numeric solve block you use to determine the shortest distance of an arbitrary point to your ellipse.
I can think of three solutions but I guess only the third one would be a real solution:
1) use a different kind of solve block with S.tc(....)=0 and MinErr(x.c,y.c)
2) provide guess values to your solve block which depend on x an y as well, not only the center of the ellipse.
3) Find an analytic way to determine the shortest distance
When using #1 or #2 I would also suggest to catch any errors in the solve block with an "on error" statement which returns a NaN vector in case of the solve block not able to find a solution.
Furthermore you can speedup the calculation abit if you don't call F(x,y) twice in your function f(x,y).
Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Werner!
Can you send the correct Mathcad 15 sheet?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
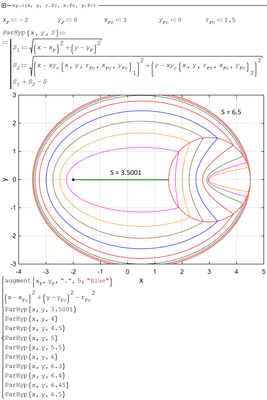
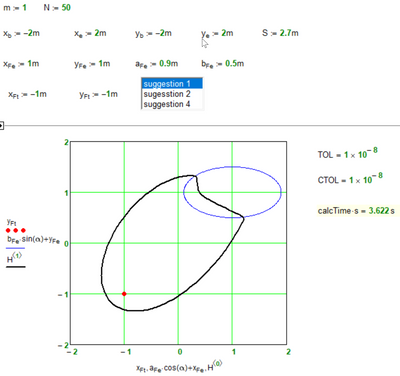
Here are the sheets corresponding which implement my suggestions #1 and #2 above.
None of the two sheets is the "correct" (analytical) one, though. I guess in any of these sheets you can find situations where wrong results may show up. But at least they seem to work OK with your setup and S=3.7. Especially the first one - in the second one the solve block seems to fail quite often, hence the many gaps in the plot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is suggestion #4 using the derivative but still a numeric solve block. Its even slower than #2 and very sensitive with respect to the provided guess value 😞
#2 and #4 seems to be that slow because the solve block quite often fails. Deriving a way to determine a better guess value depending on x an y would be mandatory.
#1 with MinErr won't ever fail and so provides the fastest performance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We can not use MinErr - xc and yc must be on the ellipse-focus. In it one constrain in the Given-Minimize block!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
We can not use MinErr - xc and yc must be on the ellipse-focus. In it one constrain in the Given-Minimize block!
Why should Minerr not be used? (xc/yc) being on the given ellipse IS a constraint in the solve block which is considered as good or bad as anything else in a numeric solve block, no matter if its used with minimize or minerr. As my suggestion #1 shows it works OK - at least with your given data - and its faster than any other approach so far.
The best solution of course would be to get rid of the numerics and derive a symbolic solution for the shortest distance of a point to an arbitrary ellipse. This would require some efforts and probably a more capable symbolic engine. But once you succeed you will have the fastest and most precise solution - good luck! 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E wrote:
@ValeryOchkov wrote:
We can not use MinErr - xc and yc must be on the ellipse-focus. In it one constrain in the Given-Minimize block!
Why should Minerr not be used? 🙂
See please the attach
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
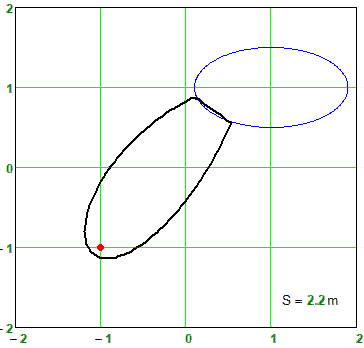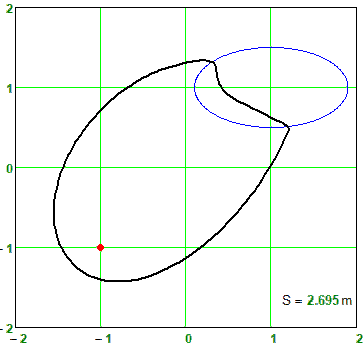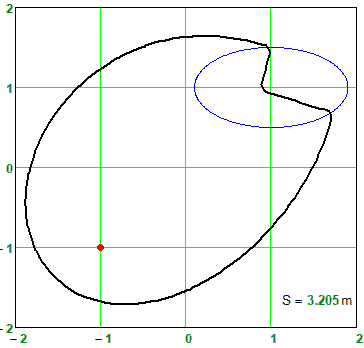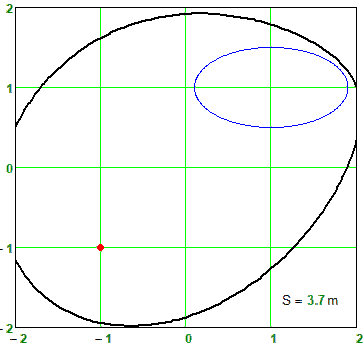
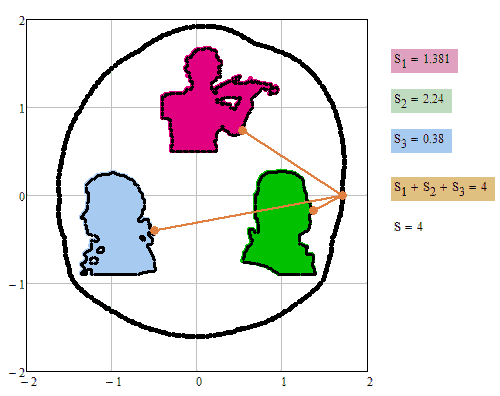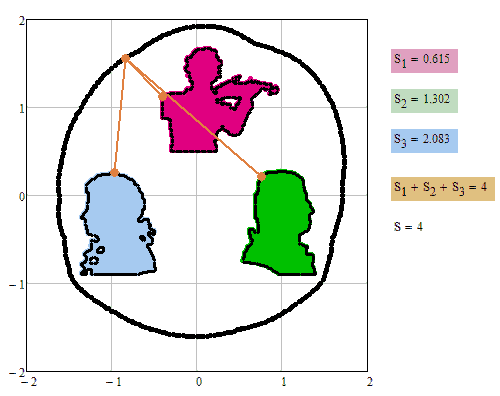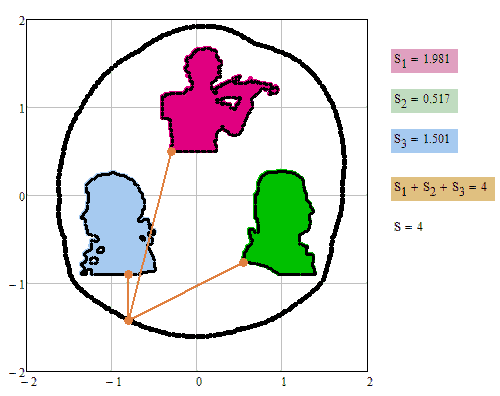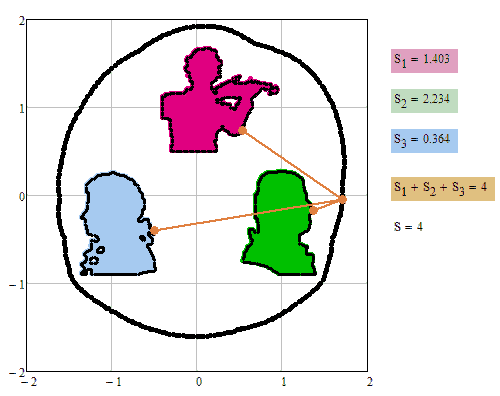
We can use the MinErr but not by S<2.2
A Boa (Python) and a rabbit (Mathcad)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I see. Instead of failing, because there is NO solution, MinErr returns an inaccurate result.
But failures like this must be expected in one way or another as long as you use numeric algorithms. Only cure would be an exact symbolic solution.
But when you use Minerr, you can "weight" your constraints and if "Point on ellipse" is more important than "sum of lenths = S", you may weight it more like shown here:
EDIT: I have integrated all three suggestions offered so far into a single worksheet for selection. So you can play around with them and add your own methods ... If you find something more efficient as #1, let us know.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One more pictures
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
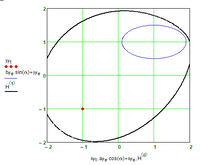
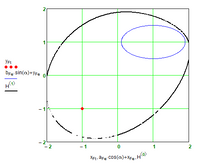
I may be wrong but didn't you deal with that kind of modifications of the ellipse definitions already in the past? Especially the second where you use two points and a constant product of lengths. BTW, how about seeing your Cassini plot as a contour plot and creating the appropriate 3D shape?
But .... can you see any practical use for these curves?
And then another idea. Why are you limiting yourself to just one ellipse as focal element and still one point (I am talking about your initial question here where the sum of the shortest distances is constant)?
You could use any shape for any of the two (or more?) "focal elements". Again I don't see any use for it but its funny to play around with them 😉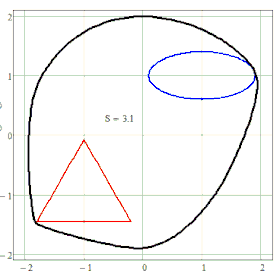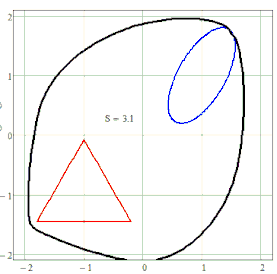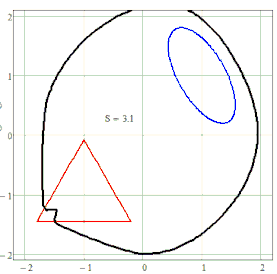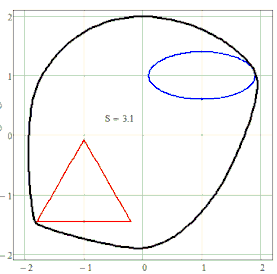
This time the gaps seem to stem from the implicitplot2D function and not from determining the shortest distance. The plots were made with a grid of N=55 resp. N=75 only to save calculation time.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>But .... can you see any practical use for these curves?
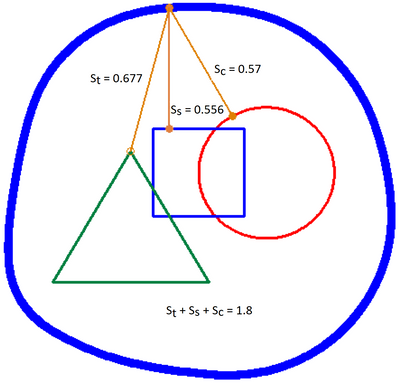
One example in my article:
Fig. 11. Ellipse with three foci: triangle, square and circle
The oval in Figure 11 is the outline of a dish (a slightly skewed “blue-rimmed saucer”) with an avant-garde geometric pattern (with our unusual tricks), which could be 3D printed at the porcelain manufactory in Meissen. This production, we recall, was founded by Count Tschirnhaus, a researcher of three-focal ellipses. A service made of such dishes would be very appropriate at a banquet on the occasion of the Fields or Abel Prizes, which are considered the most prestigious prizes in mathematics. They are often called the Nobel Prizes for this queen of sciences. There are many guesses why Alfred Nobel himself did not establish a prize in mathematics, replacing it with a rather controversial and scandalous peace prize.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah yes, I now remember your post on porcelain manufacturing. There may be easier ways to create irregular ovals, but why not.
It's a little questionable, though, whether creating plates for the Fields award ceremony is a viable business model 😉
Maybe it could be made more interesting for a broader market by personalization using a silhouette 🙂
🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>But .... can you see any practical use for these curves?
A plate for a banquet is not serious.
The main practical goal is to give Werner the pleasure of solving an interesting problem. And also admire us as he does it!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Whose profile is this? Who is it?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Whose profile is this? Who is it?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Whose profile is this? Who is it?
Its Johann Joachim Kändler (1706 – 1775). -> https://en.wikipedia.org/wiki/Johann_Joachim_K%C3%A4ndler
I got inspired and triggered by "porcelain" 😉
But I admit that using a Mozart silhouette used by Augarten Porzellan would have been a more patriotic choice. On the other hand it would have been much more cheesy and clichéd. 😉
https://www.interismo.at/augarten/schaelchen-mozart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why not
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can try any shapes you like.
Mathcad is dispassionate about this, but I prefer musicians like Strauss Jr., Mozart and Haydn instead of a warmonger.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Propaganda is a great thing. There are many examples. One is above. Here is another example. Propaganda made the whole world believe that Mozart was an Austrian and Hitler a German.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I consider this forum not the right place for any political statements.
But just to put it right: Mozart actually was Austrian.
You probably confuse it with Beethoven. Many People think that Beethoven was Austrian because he spent more time of living in Austria (Vienna) and most of his brilliant work was created in Vienna. Nonetheless he was born in Germany (Bonn) and lived there up to his twenties.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, let's not talk about politics. Let's talk about the most popular Mozart melody and about women.
Пора по бабам, пора по бабам, пора по бабам, по бабам, по бабам...
Я вам дам даром, я вам дам даром, я вам дам даром, дам даром, дам даром...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_Eнаписал:Но если говорить правильно: Моцарт на самом делебылавстрийцем.
Невозможно объяснить на английском или немецком языках
Только на русском языке
В русском языке есть два слова - немец и германец.
Моцарт не был ни австрийцем, ни германцем. Он был немцем - выходцем из той части Европы, где говорили на немецком, датском, голландском и прочих подобных языках.
Но по большому счету гении не имеют национальности.
Вернер очень талантлив в математике. Поэтому он не австриец, а гражданин Мира!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
@Werner_E wrote:But just to put it right: Mozart actually was Austrian.
It is impossible to explain in English or in Deutsch
Only in Russian
If that would be true, it would not make any sense to try to translate your posting via Google or DeepL. Nonetheless I tried and all I can say is, that every Russian, German., Austrian, ... etc. IS, of course, a world citizen, but nonetheless, as long as we divide and divide the world as arbitrarily as we do, as long they are Russians, Germans, Austrians, etc., as well (or primarily - depending on your point of view).