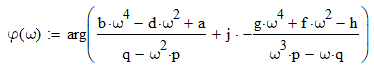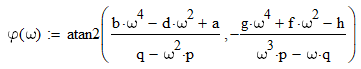Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Node analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Node analysis
Hi!
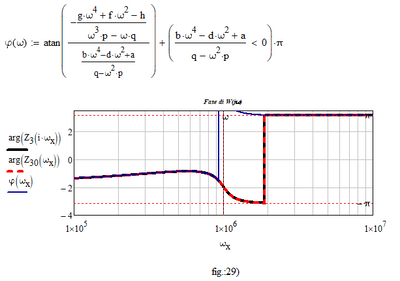
Why, in figure 29 of the attached worksheet, do the phases not coincide? And in general, if I have made any mistakes please let me know. Thanks very much to those who will answer.
Solved! Go to Solution.
- Labels:
-
Electrical_Engineering
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
Hi!
Why, in figure 29 of the attached worksheet, do the phases not coincide?
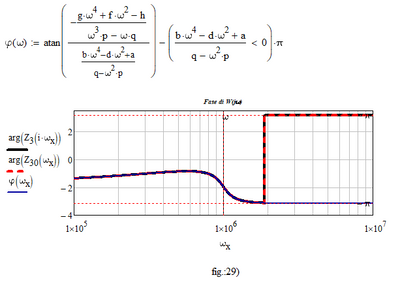
Because its wrong to just use "atan (Im(z)/Re(z))" to get the phase for any complex number z. To get the correct result you'll have to add or subtract pi if Re(z)<0!
Adding pi gives you the phase in the range ]-pi/2; 3 pi /2] and looks like this:
Subtracting pi forces the phase to ]-3 pi /2; pi/2)
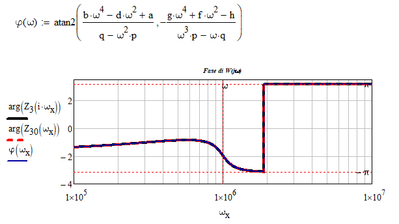
You may use "atan2" instead of "atan" in your function phi to get the very same results as you get with "arg", that is a phase in }-pi; pi]
Using atan2 also has the advantage that the case of Re(z)=0 is handled correctly and does not throw an error!
Of course "arg" would do the job equally well 😉
BTW, to avoid jump discontinuities in the phase plot you can use the "phasecor( )" function but you have to turn the continuos function into vectors for plotting.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Right, we talked about it a while ago, but I had just forgotten it. Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator