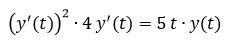Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Nonlinear 1°ord differential equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nonlinear 1°ord differential equation
Hi everybody,
how can I solve this equation?
I found problems because of the derivative function squared. I need to collect the term derivative not squared...
Thanks
Bye
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can turn the non-linear y'(t)^2 + 4y'(t) = 5ty(t) into two simultaneous linear ode's:
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm squared.... Seems more like to the 3rd power.
You have (y'(t))^2 and mutiply that with 4 y'(t), that gives 4*(y'(t))^3...
Do you need a symbolic solution, or can you settle for a numeric approximation.
Either way: what are the initial values? [ y(0), y'(0)]
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Found it.
Try y(t)=+/-(1/8)*sqrt(10)*t^2.
The third solution is y(t)=0, but I guess you weren't looking for that.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's a possible workaround for a numerical solution, both Prime and real Mathcad:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm so sorry because I wrote "(y'(t)^2) * 4y'(t)" instead of "(y'(t)^2) + 4y'(t)" that it changes a lot...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From Mathcad's documentation of "odesolve":
The ODE must be linear in its highest derivative term,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Does y(t) describe a physical phenomenon as a function of time? Or is this a made-up DE?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can turn the non-linear y'(t)^2 + 4y'(t) = 5ty(t) into two simultaneous linear ode's:
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to find y(0)=1?
z(0)=0, How about z(0)=-4?
Tokoro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
y(0)=1 was an arbitrary choice on my part, as no initial conditions were specified in the original question.
z(0)=-4 gives rise to a rapidly decreasing y with time (and with y(0)=1). If this is what is expected from the model then fine! Personally, I think it’s probably safer to stick with z(0)=0.
Alan